题目内容
7.已知关于x的一元二次方程x2+2kx+k2-k-2=0有两个不相等的实数根.(1)求实数k的取值范围;
(2)已知x=0是方程的一个根,请求出方程的另一个根.
分析 (1)根据已知得出△>0,求出即可.
(2)把x=0代入方程,求出k的值,把k的值代入方程,求出方程的另一个根即可.
解答 解:(1)由题意,知△>0,
所以,(2k)2-4(k2-k-2)=4k+8>0,
解得k>-2.
(2)把x=0代入方程,得k2-k-2=0,
解得 k=-1或k=2.
当k=2时,原方程为x2+4x=0,
解得,x1=0,x2=-4,
当k=-1时,原方程为x2-2x=0,
解得,x1=0,x2=2,
所以当k=2,方程的另一个根是-4;k=-1,方程的另一个根是2.
点评 本题考查了根的判别式的应用,注意:一元二次方程ax2+bx+c=0(a、b、c为常数,a≠0),①当b2-4ac>0时,方程有两个不相等的实数根;②当b2-4ac=0时,方程有两个相等的实数根,③当b2-4ac<0时,方程没有实数根.

练习册系列答案
相关题目
15.下列计算正确的是( )
| A. | 3a2-a2=3 | B. | a6÷a2=a3 | C. | (a2)3=a5 | D. | a2•a3=a5 |
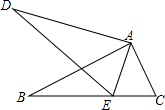 如图,在△ABC和△ADE中,点E在BC边上,∠BAC=∠DAE,∠B=∠D,AB=AD.
如图,在△ABC和△ADE中,点E在BC边上,∠BAC=∠DAE,∠B=∠D,AB=AD.