题目内容
3.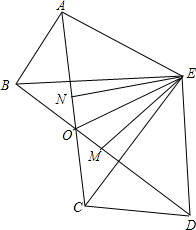 如图,BE=CE,AB=DC,∠ABE=∠DCE,连接AC、DB交于点O,连接OE,EM、EN分别平分∠AEC和∠BED.求证:
如图,BE=CE,AB=DC,∠ABE=∠DCE,连接AC、DB交于点O,连接OE,EM、EN分别平分∠AEC和∠BED.求证:(1)∠CAE=∠BDE;
(2)EN=EM.
分析 (1)利用“SAS”证得△ABE≌△DCE,得出∠AEB=∠CED,AE=DE,再进一步证得△ACE≌△DBE,即可得出结论;
(2)由△ACE≌△DBE,得出∠EAC=∠EDB,∠AEC=∠DEB,由角平分线的性质得出∠AEN=∠DEM,证得△ANE≌△DME,得出结论.
解答 证明:(1)在△ABE和△DCE中,
$\left\{\begin{array}{l}{BE=CE}\\{∠ABE=∠DCE}\\{AB=DC}\end{array}\right.$,
∴△ABE≌△DCE,
∴∠AEB=∠CED,AE=DE,
∴∠AEC=∠DEB,
在△ACE和△DBE中,
$\left\{\begin{array}{l}{AE=ED}\\{∠AEC=∠DEB}\\{EC=EB}\end{array}\right.$,
∴△ACE≌△DBE,
∴∠CAE=∠BDE;
(2)∵△ACE≌△DBE,
∴∠CAE=∠BDE,∠AEC=∠DEB,
∵EM、EN分别平分∠AEC和∠BED,
∴∠AEN=∠DEM,
在△ANE和△DME中,
$\left\{\begin{array}{l}{∠NAE=∠MED}\\{AE=ED}\\{∠AEN=∠DEM}\end{array}\right.$,
∴△ANE≌△DME,
∴EN=EM.
点评 此题考查三角形全等的判定与性质,角平分线的性质,掌握三角形全等的判定方法是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.下列计算正确的是( )
| A. | 3a2-a2=3 | B. | a6÷a2=a3 | C. | (a2)3=a5 | D. | a2•a3=a5 |
 如图,AC为一根电线杆,钢缆AB的长为5m,钢缆底端B与电线底端C的距离为3m,在D处有一个蜘蛛窝.两只蜘蛛同时从点D出发以同样的速度沿路径D-A-B和路径D-C-B织网,结果正好在点B相遇,求蜘蛛窝D的高度.
如图,AC为一根电线杆,钢缆AB的长为5m,钢缆底端B与电线底端C的距离为3m,在D处有一个蜘蛛窝.两只蜘蛛同时从点D出发以同样的速度沿路径D-A-B和路径D-C-B织网,结果正好在点B相遇,求蜘蛛窝D的高度.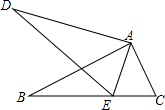 如图,在△ABC和△ADE中,点E在BC边上,∠BAC=∠DAE,∠B=∠D,AB=AD.
如图,在△ABC和△ADE中,点E在BC边上,∠BAC=∠DAE,∠B=∠D,AB=AD. 如图,在Rt△ABC中,∠C=90°,AC:BC=1:2,在Rt△ABC中有多个依次排队的正方形DCFE,GFHK,PHTQ…,如果第一个正方形的边长为a,则第2012个正方形的边长应为$\frac{{2}^{2012}}{{3}^{2012}}$.
如图,在Rt△ABC中,∠C=90°,AC:BC=1:2,在Rt△ABC中有多个依次排队的正方形DCFE,GFHK,PHTQ…,如果第一个正方形的边长为a,则第2012个正方形的边长应为$\frac{{2}^{2012}}{{3}^{2012}}$.