题目内容
8.已知x-y=3,且x>2,y<1,求x+y的范围.分析 首先把x-y=3变形为y=x-3,再根据等量代换可得x-3<1,然后可得x的取值范围,进而可得y的取值范围,然后计算x+y即可.
解答 解:∵x-y=3,
∴y=x-3,
∵y<1,
∴x-3<1,
解得:x<4,
∵x>2,
∴2<x<4,
∴2-3<x-3<4-3,
∴-1<y<1,
∴1<x+y<5.
点评 此题主要考查了不等式的变形,关键是掌握不等式的两边同时加上(或减去)同一个数或同一个含有字母的式子,不等号的方向不变.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案
相关题目
3.若x-|x|=0,则$\sqrt{{x}^{2}}$=( )
| A. | x | B. | -|x| | C. | -x | D. | x2 |
 据统计资料,甲、乙两种作物的单位面积产值的比是1:2,现在要把一块长AB为200米、宽AD为100米的长方形土地,分为两块土地,分别种植两种作物,使甲、乙两种作物的总产量得比是3:4.如图,若甲、乙两种作物的种植区域分别为长方形ABFE和EFCD,此时设AE=x m,ED=y m,列方程组求x、y的值并写出种植甲、乙两种作物的面积.
据统计资料,甲、乙两种作物的单位面积产值的比是1:2,现在要把一块长AB为200米、宽AD为100米的长方形土地,分为两块土地,分别种植两种作物,使甲、乙两种作物的总产量得比是3:4.如图,若甲、乙两种作物的种植区域分别为长方形ABFE和EFCD,此时设AE=x m,ED=y m,列方程组求x、y的值并写出种植甲、乙两种作物的面积. 如图,已知在△ABC中,∠BAC=90°,AD⊥BC于点D,E是AD上一点,试说明∠C与∠DEB的大小关系.
如图,已知在△ABC中,∠BAC=90°,AD⊥BC于点D,E是AD上一点,试说明∠C与∠DEB的大小关系.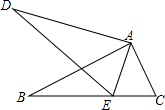 如图,在△ABC和△ADE中,点E在BC边上,∠BAC=∠DAE,∠B=∠D,AB=AD.
如图,在△ABC和△ADE中,点E在BC边上,∠BAC=∠DAE,∠B=∠D,AB=AD.