题目内容
5.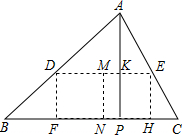 如图,△ABC是一块锐角三角形余料,边长BC=120cm,高AP=90cm,现在要把它加工成长方形零件DFHE,且满足FH=2DF,F、H在BC上,D、E分别在AB、AC上,求短边DF的长.
如图,△ABC是一块锐角三角形余料,边长BC=120cm,高AP=90cm,现在要把它加工成长方形零件DFHE,且满足FH=2DF,F、H在BC上,D、E分别在AB、AC上,求短边DF的长.
分析 设DF=xcm,则DE=2xcm,AD=(90-x)cm,由△ADE∽△ABC列出比例式求解即可.
解答 解:设DF=xcm,
则DE=2xcm,AD=(90-x)cm,
∵DE∥BC,
∴△ADE∽△ABC,
∴$\frac{AK}{AD}=\frac{DE}{BC}$,
∴$\frac{90-x}{90}=\frac{2x}{120}$,
∴x=36,
∴DF的长为36cm.
点评 本题考查了相似三角形的应用及矩形的性质,解题的关键是能够根据矩形的性质表示出有关线段的长,并利用相似三角形列出正确的比例式求解.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
16.若角α、β是直角三角形的两个锐角,则$\frac{sinα}{cosβ}$-tan$\frac{α+β}{2}$的值为( )
| A. | 0 | B. | 1 | C. | 1-$\sqrt{2}$ | D. | $\frac{\sqrt{2}}{2}$-1 |
13. 二次函数y=ax2+bx+c的图象如图所示(a、b、c为常数),则函数y=(4ac-b2)x+abc和y=$\frac{2a+b}{x}$在同一平面直角坐标系中的图象,可能是( )
二次函数y=ax2+bx+c的图象如图所示(a、b、c为常数),则函数y=(4ac-b2)x+abc和y=$\frac{2a+b}{x}$在同一平面直角坐标系中的图象,可能是( )
 二次函数y=ax2+bx+c的图象如图所示(a、b、c为常数),则函数y=(4ac-b2)x+abc和y=$\frac{2a+b}{x}$在同一平面直角坐标系中的图象,可能是( )
二次函数y=ax2+bx+c的图象如图所示(a、b、c为常数),则函数y=(4ac-b2)x+abc和y=$\frac{2a+b}{x}$在同一平面直角坐标系中的图象,可能是( )| A. |  | B. |  | C. |  | D. |  |
14.下列运算正确的是( )
| A. | 3x+3y=6xy | B. | -y2-y2=0 | C. | 3(x+8)=3x+8 | D. | -(6x+2y)=-6x-2y |
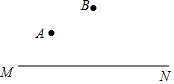 A、B两厂在公路MN同侧,拟在公路边建一货场C,若由B厂独家兴建,并考虑B厂的利益,则要求货场离B厂最近,请在图中作出此时货场C的位置,并说出这样做的道理.
A、B两厂在公路MN同侧,拟在公路边建一货场C,若由B厂独家兴建,并考虑B厂的利益,则要求货场离B厂最近,请在图中作出此时货场C的位置,并说出这样做的道理. 如图所示,点A在直线a外,点B在直线a上,在直线a上找一点P,使AP+BP最小的点P有1个,其位置是B点.
如图所示,点A在直线a外,点B在直线a上,在直线a上找一点P,使AP+BP最小的点P有1个,其位置是B点.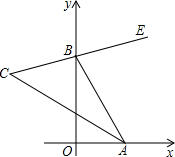 如图,在直角坐标系中,点A、B分别在射线OX、OY上移动,BE是∠ABY的角平分线,BE的反向延长线与∠OAB的平分线相交于点C,试问∠ACB的大小是否发生变化?如果保持不变,请给出证明.
如图,在直角坐标系中,点A、B分别在射线OX、OY上移动,BE是∠ABY的角平分线,BE的反向延长线与∠OAB的平分线相交于点C,试问∠ACB的大小是否发生变化?如果保持不变,请给出证明. 如图,已知等腰直角三角ACB的边AC=BC=a,等腰直角三角形BED的边BE=DE=b
如图,已知等腰直角三角ACB的边AC=BC=a,等腰直角三角形BED的边BE=DE=b