题目内容
17. 如图,已知等腰直角三角ACB的边AC=BC=a,等腰直角三角形BED的边BE=DE=b
如图,已知等腰直角三角ACB的边AC=BC=a,等腰直角三角形BED的边BE=DE=b且a<b,点C、B、E放置在一条直线上,联结AD.
(1)求△ABD的面积;
(2)如果P是线段CE中点,联结AP,DP得到△APD,求△APD的面积;
(3)(2)中的△APD与△ABD面积那个大?(结果都可用a、b代数式表示,并化简.)
分析 (1)直接根据S△ABD=S梯形ACED-S△ABC-S△BDE进行计算即可;
(2)根据S△APD=S梯形ACED-S△APC-S△DEP进行计算即可;
(3)分别求出△APD与△ABD的面积,利用作差法进行比较即可.
解答 解:(1)S△ABD=S梯形ACED-S△ABC-S△BDE
=$\frac{1}{2}$(a+b)(a+b)-$\frac{1}{2}$a2-$\frac{1}{2}$b2
=ab;
(2)如图,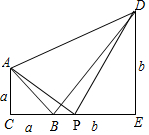
∵P为CE的中点,
∴CP=EP=$\frac{1}{2}$(a+b),
∴S△APD=S梯形ACED-S△APC-S△DEP
=$\frac{1}{2}$(a+b)(a+b)-$\frac{1}{2}$a•$\frac{a+b}{2}$-$\frac{1}{2}$b•$\frac{a+b}{2}$
=$\frac{1}{2}$a2+ab+$\frac{1}{2}$b2-$\frac{1}{4}$a2-$\frac{1}{4}$ab-$\frac{1}{4}$ab-$\frac{1}{4}$b2
=$\frac{1}{4}$(a+b)2;
(3)∵S△APD-S△ABD=$\frac{1}{4}$(a+b)2-ab=$\frac{1}{4}$(a-b)2>0,
∴△APD的面积大.
点评 本题考查的是等腰直角三角形及三角形的面积、梯形的面积、整式的混合运算,熟知梯形及三角形的面积公式和割补法求面积是解答此题的关键.

练习册系列答案
相关题目
8.已知函数f(x)=ax2+2ax+4(0<a<3),若x1<x2,x1+x2=1-a,则( )
| A. | f(x1)<f(x2) | B. | f(x1)=f(x2) | ||
| C. | f(x1)>f(x2) | D. | f(x1)与f(x2)的大小不能确定 |
2.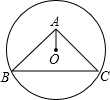 在等腰直角△ABC中,∠BAC=90°,BC=6,⊙O的圆心O在△ABC内部,且经过B、C两点,若OA=1,则⊙O的半径为( )
在等腰直角△ABC中,∠BAC=90°,BC=6,⊙O的圆心O在△ABC内部,且经过B、C两点,若OA=1,则⊙O的半径为( )
 在等腰直角△ABC中,∠BAC=90°,BC=6,⊙O的圆心O在△ABC内部,且经过B、C两点,若OA=1,则⊙O的半径为( )
在等腰直角△ABC中,∠BAC=90°,BC=6,⊙O的圆心O在△ABC内部,且经过B、C两点,若OA=1,则⊙O的半径为( )| A. | $\sqrt{10}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{13}$ | D. | 3$\sqrt{2}$ |
9.我校为了纪念“一二•九”举办了八年级红歌合唱比赛,为了保证这次比赛的公正性,规定:参赛班级的基本素养、精神面貌、服装三项打分分别按5:3:2的比例计入总评成绩.二班、三班、五班的基本素养、精神面貌、服装的打分如下表,计算哪个班是第一名?
| 基本素养 | 精神面貌 | 服装 | |
| 二班 | 90 | 96 | 93 |
| 三班 | 90 | 90 | 96 |
| 五班 | 96 | 94 | 90 |
6. 如图,若∠A=27°,∠B=45°,∠C=38°,则∠DFE等于( )
如图,若∠A=27°,∠B=45°,∠C=38°,则∠DFE等于( )
 如图,若∠A=27°,∠B=45°,∠C=38°,则∠DFE等于( )
如图,若∠A=27°,∠B=45°,∠C=38°,则∠DFE等于( )| A. | 110° | B. | 115° | C. | 120° | D. | 125° |
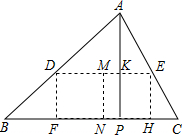 如图,△ABC是一块锐角三角形余料,边长BC=120cm,高AP=90cm,现在要把它加工成长方形零件DFHE,且满足FH=2DF,F、H在BC上,D、E分别在AB、AC上,求短边DF的长.
如图,△ABC是一块锐角三角形余料,边长BC=120cm,高AP=90cm,现在要把它加工成长方形零件DFHE,且满足FH=2DF,F、H在BC上,D、E分别在AB、AC上,求短边DF的长.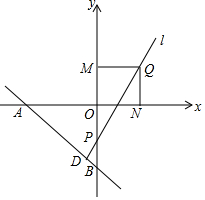 如图,在平面直角坐标系中,A(-8,0),B(0,-8),D为直线AB上一点,且D点横坐标为-2,y轴上有一动点P,直线l经过D、P两点.
如图,在平面直角坐标系中,A(-8,0),B(0,-8),D为直线AB上一点,且D点横坐标为-2,y轴上有一动点P,直线l经过D、P两点.