题目内容
13．
（1）实数a、b在数轴上的位置如图所示，请化简：|a|-$\sqrt{a^2}-\sqrt{b^2}$；（2）利用不等式性质将6x+5＜4x-3化为x＞a或或x＜a的形式．
分析 （1）根据数轴上点的位置判断出a与b的大小，利用二次根式的性质及绝对值的代数意义化简，计算即可得到结果；
（2）利用不等式的基本性质两边减去4x+5，再两边除以2即可得出解集．
解答 解：（1）∵a＜0＜b，
∴原式=-a-（-a）-b=-b；
（2）不等式两边减去4x+5得：2x＜-8，
两边除以2得：x＜-4．
点评 此题考查了实数与数轴，以及二次根式的性质与化简，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
3．下列各式一定是二次根式的是（ ）
| A． | $\sqrt{-7}$ | B． | $\sqrt{x}$ | C． | $\sqrt{{x^2}+{y^2}}$ | D． | $\root{3}{6}$ |
4．⊙O1的半径为3厘米，⊙O2的半径为2厘米，圆心距O1O2=4厘米，这两圆的位置关系是（ ）
| A． | 内含 | B． | 内切 | C． | 相交 | D． | 外切 |
1．在下列二次根式中，x的取值范围是x＞3的是（ ）
| A． | $\sqrt{3-x}$ | B． | $\sqrt{x+3}$ | C． | $\sqrt{x-3}$ | D． | $\sqrt{\frac{1}{x-3}}$ |
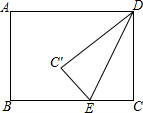如图，矩形ABCD中，AB=6，BC=8，点E是射线CB上的一个动点，把△DCE沿DE折叠，点C的对应点为C′．
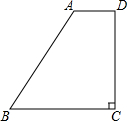如图，有一块梯形空地ABCD可供停车，AD∥BC，∠C=90°，∠B=53°，AD=1.6m，CD=5.2m，现有一辆长4.9m，宽1.9m的汽车需要完全停入梯形区域，请你设计一种停车方案，并通过计算说明理由．（参考数据：sin53°≈$\frac{4}{5}$，cos53°≈$\frac{3}{5}$，tan53°≈$\frac{4}{3}$）
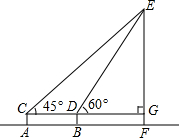如图，为了测得铁塔的高度，小莹利用自制的测角仪，在C点测得塔顶E的仰角为45°，在D点测得塔顶E的仰角为60°，已知测角仪AC的高为1.6米，CD的长为6米，CD所在的水平线CG⊥EF于点G，铁塔EF的高为（10.6+3$\sqrt{3}$）米．（结果用带根号的式子表示）
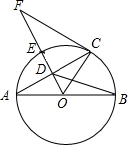如图，AB是⊙O的直径，OD垂直弦AC于点D，OD的延长线交⊙O 于点E，与过点C的⊙O的切线交于点F，已知OD=3，DE=2．