题目内容
8.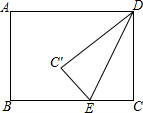 如图,矩形ABCD中,AB=6,BC=8,点E是射线CB上的一个动点,把△DCE沿DE折叠,点C的对应点为C′.
如图,矩形ABCD中,AB=6,BC=8,点E是射线CB上的一个动点,把△DCE沿DE折叠,点C的对应点为C′.(1)若点C′刚好落在对角线BD上时,BC′=4;
(2)若点C′刚好落在线段AB的垂直平分线上时,求CE的长;
(3)若点C′刚好落在线段AD的垂直平分线上时,求CE的长.
分析 (1)根据点B,C′,D在同一直线上得出BC′=BD-DC′=BD-DC求出即可;
(2)利用垂直平分线的性质得出CC′=DC′=DC,则△DC′C是等边三角形,进而利用勾股定理得出答案;
(3)利用①当点C′在矩形内部时,②当点C′在矩形外部时,分别求出即可.
解答 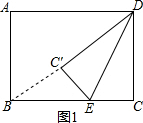 解:(1)如图1,∵点B,C′,D在同一直线上,
解:(1)如图1,∵点B,C′,D在同一直线上,
∴BC′=BD-DC′=BD-DC=10-6=4;
故答案为:4;
(2)如图2,连接CC′,
∵点C′在AB的垂直平分线上,
∴点C′在DC的垂直平分线上,
∴CC′=DC′=DC,则△DC′C是等边三角形,
设CE=x,易得DE=2x,
由勾股定理得:(2x)2-x2=62,
解得:x=2$\sqrt{3}$,
即CE的长为2$\sqrt{3}$;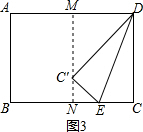
(3)作AD的垂直平分线,交AD于点M,交BC于点N,分两种情况讨论:
①当点C′在矩形内部时,如图3,
∵点C′在AD的垂直平分线上,
∴DM=4,
∵DC′=6,
由勾股定理得:MC′=2$\sqrt{5}$,
∴NC′=6-2$\sqrt{5}$,
设EC=y,则C′E=y,NE=4-y,
故NC′2+NE2=C′E2,
即(6-2$\sqrt{5}$)2+(4-y)2=y2,
解得:y=9-3$\sqrt{5}$,
即CE=9-3$\sqrt{5}$;
②当点C′在矩形外部时,如图4,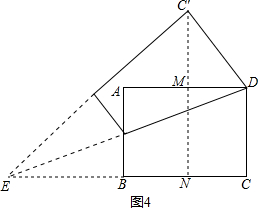
∵点C′在AD的垂直平分线上,
∴DM=4,
∵DC′=6,
由勾股定理得:MC′=2$\sqrt{5}$,
∴NC′=6+2$\sqrt{5}$,
设EC=z,则C′E=a,NE=z-4
故NC′2+NE2=C′E2,
即(6+2$\sqrt{5}$)2+(z-4)2=z2,
解得:z=9+3$\sqrt{5}$,
即CE=9+3$\sqrt{5}$,
综上所述:CE的长为9±3$\sqrt{5}$.
点评 此题主要考查了矩形的性质、翻折变换的性质、勾股定理等知识;利用数形结合以及分类讨论得出是解题关键.

 学业测评一课一测系列答案
学业测评一课一测系列答案| A. | $\sqrt{18}$ | B. | $\sqrt{20}$ | C. | $\sqrt{48}$ | D. | $\sqrt{\frac{1}{2}}$ |
 如图,AC=AD,BC=BD,则( )
如图,AC=AD,BC=BD,则( )| A. | CD垂直平分AD | B. | AB垂直平分CD | C. | CD平分∠ACB | D. | 以上结论均不对 |
| A. | $\sqrt{4x}$ | B. | $\sqrt{\frac{1}{x}}$ | C. | $\sqrt{{x}^{2}+{y}^{2}-2xy}$ | D. | $\sqrt{{x}^{2}-{y}^{2}}$ |

 (1)实数a、b在数轴上的位置如图所示,请化简:|a|-$\sqrt{a^2}-\sqrt{b^2}$;
(1)实数a、b在数轴上的位置如图所示,请化简:|a|-$\sqrt{a^2}-\sqrt{b^2}$; 已知,一次函数y=-$\frac{3}{4}$x+6的图象与x轴交于A,与y轴交于C,以O,A,C为顶点在第一象限作矩形OABC.
已知,一次函数y=-$\frac{3}{4}$x+6的图象与x轴交于A,与y轴交于C,以O,A,C为顶点在第一象限作矩形OABC.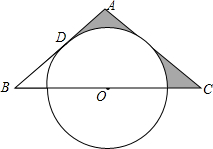 在△ABC中,AB=AC,O是BC中点,BC=12$\sqrt{3}$cm,AB与⊙O相切于点D,AD:DB=1:3
在△ABC中,AB=AC,O是BC中点,BC=12$\sqrt{3}$cm,AB与⊙O相切于点D,AD:DB=1:3 已知:如图,AB是⊙O的直径,BC切⊙O于B,AC交⊙O于P,D为BC边的中点,连接DP.
已知:如图,AB是⊙O的直径,BC切⊙O于B,AC交⊙O于P,D为BC边的中点,连接DP.