题目内容
10.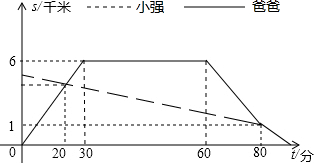 小强的爸爸从家骑自行车去图书馆借书,途中遇到了从图书馆步行回家的小强,爸爸借完书后迅速回家,途中追上了小强,便用自行车载上小强一起回家,结果爸爸比自己单独骑车回家晚到1分钟,两人与家的距离S(千米)和爸爸从家出发后的时间t(分钟)之间的关系如图所示.
小强的爸爸从家骑自行车去图书馆借书,途中遇到了从图书馆步行回家的小强,爸爸借完书后迅速回家,途中追上了小强,便用自行车载上小强一起回家,结果爸爸比自己单独骑车回家晚到1分钟,两人与家的距离S(千米)和爸爸从家出发后的时间t(分钟)之间的关系如图所示.(1)图书馆离家有多少千米?
(2)爸爸和小强第一次相遇时,离家多少千米?
(3)爸爸载上小强后一起回家的速度是多少?
分析 (1)根据折线给出的信息可知:图书馆离家有6千米;
(2)先计算爸爸:当0≤t≤30时,直线的解析式:s=$\frac{1}{5}$t,把t=20代入即可;
(3)求爸爸当60≤t≤80时独自返回,直线BC的解析式为:s=-$\frac{1}{4}$t+21,并计算当s=0时,t=84,即如果爸爸独自骑车回家,是在离家84分钟的时候到家,根据题意,爸爸载上小强后晚到家1分钟,爸爸与小强同回家,一起在5分钟走了1千米,由此计算速度即可.
解答  解:(1)由图形得:图书馆离家有6千米;
解:(1)由图形得:图书馆离家有6千米;
(2)对于爸爸:当0≤t≤30时,去图书馆,
设直线OA的解析式为:s=kt,
把A(30,6)代入得:30k=6,
k=$\frac{1}{5}$,
则直线OA的解析式为:s=$\frac{1}{5}$t,
当t=20时,s=$\frac{1}{5}$×20=4;
答:爸爸和小强第一次相遇时,离家4千米;
(3)对于爸爸,当30<t≤60时在借书,此时s=6,
当60≤t≤80时独自返回,设直线BC的解析式为:s=kt+b,
把B(60,6)、C(80,1)代入得:$\left\{\begin{array}{l}{60k+b=6}\\{80k+b=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{1}{4}}\\{b=21}\end{array}\right.$,
∴直线BC的解析式为:s=-$\frac{1}{4}$t+21,
令s=0时,t=84,
即如果爸爸独自骑车回家,是在离家84分钟的时候到家,根据题意,爸爸载上小强后晚到家1分钟,爸爸与小强同回家,一起在5分钟走了1千米,
t=$\frac{1}{5}$=0.2,
答:爸爸载上小强后一起回家的速度为0.2千米/分钟.
点评 本题考查了根据折线统计图提供的信息,解决行程问题,与一次函数的解析式相结合,明确时间、速度、路程的关系是关键.

 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案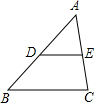 如图,在△ABC中,点D、E分别是AB、AC的中点,则下列结论:①BC=3DE;②△ADE∽△ABC;$③\frac{AD}{AE}=\frac{AB}{AC}$;④$\frac{三角形ADE面积}{四边形BCED的面积}=\frac{1}{3}$,其中正确的有( )
如图,在△ABC中,点D、E分别是AB、AC的中点,则下列结论:①BC=3DE;②△ADE∽△ABC;$③\frac{AD}{AE}=\frac{AB}{AC}$;④$\frac{三角形ADE面积}{四边形BCED的面积}=\frac{1}{3}$,其中正确的有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
| A. | 0.30067×106 | B. | 3.0067×105 | C. | 3.0067×104 | D. | 30.067×104 |
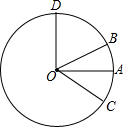 如图,点A,点B在以点O为圆心的圆上,且∠AOB=30°,如果甲机器人从点A出发沿着圆周按顺时针方向以每秒5°的速度行驶,乙机器人从点B出发沿着圆周按逆时针方向行驶,速度是甲机器人的2倍,经过一段时间后,甲、乙分别运动到点C,点D,当乙机器人第一次到达点B时,甲、乙同时停止运动.
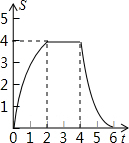
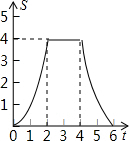
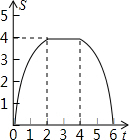
如图,点A,点B在以点O为圆心的圆上,且∠AOB=30°,如果甲机器人从点A出发沿着圆周按顺时针方向以每秒5°的速度行驶,乙机器人从点B出发沿着圆周按逆时针方向行驶,速度是甲机器人的2倍,经过一段时间后,甲、乙分别运动到点C,点D,当乙机器人第一次到达点B时,甲、乙同时停止运动. 如图,边长为4个单位长度的正方形ABCD的边AB与等腰直角三角形EFG的斜边FG重合,△EFG以每秒1个单位长度的速度沿BC向右匀速运动(保持FG⊥BC),当点E运动到CD边上时△EFG停止运动,设△EFG的运动时间为t秒,△EFG与正方形ABCD重叠部分的面积为S,则S关于t的函数大致图象为( )
如图,边长为4个单位长度的正方形ABCD的边AB与等腰直角三角形EFG的斜边FG重合,△EFG以每秒1个单位长度的速度沿BC向右匀速运动(保持FG⊥BC),当点E运动到CD边上时△EFG停止运动,设△EFG的运动时间为t秒,△EFG与正方形ABCD重叠部分的面积为S,则S关于t的函数大致图象为( )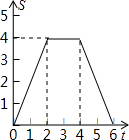
 在四边形ABCD中,对角线AC与BD相交于点O,∠CAB=∠CBD,若BC=3,求AC•CE的值.
在四边形ABCD中,对角线AC与BD相交于点O,∠CAB=∠CBD,若BC=3,求AC•CE的值. 把一个斜边长为10cm的含45°角的直角三角板放在三条互相平行的直线a,b,c,且直线a,b的距离和直线b,c之间的距离都是d,求d的值.
把一个斜边长为10cm的含45°角的直角三角板放在三条互相平行的直线a,b,c,且直线a,b的距离和直线b,c之间的距离都是d,求d的值.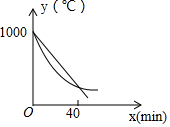 某研究所将某种材料加热到1000℃时停止加热,并立即将材料分为A、B两组,采用不同工艺做降温对比实验,设降温开始后经过xmin时,A、B两组材料的温度分别为yA℃、yB℃;yA、yB与x的函数关系式分别为yA=kx+b,yB=$\frac{1}{4}$(x-60)2+m(部分图象如图所示,当x=40时,两组材料的温度相同).
某研究所将某种材料加热到1000℃时停止加热,并立即将材料分为A、B两组,采用不同工艺做降温对比实验,设降温开始后经过xmin时,A、B两组材料的温度分别为yA℃、yB℃;yA、yB与x的函数关系式分别为yA=kx+b,yB=$\frac{1}{4}$(x-60)2+m(部分图象如图所示,当x=40时,两组材料的温度相同).