题目内容
20.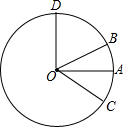 如图,点A,点B在以点O为圆心的圆上,且∠AOB=30°,如果甲机器人从点A出发沿着圆周按顺时针方向以每秒5°的速度行驶,乙机器人从点B出发沿着圆周按逆时针方向行驶,速度是甲机器人的2倍,经过一段时间后,甲、乙分别运动到点C,点D,当乙机器人第一次到达点B时,甲、乙同时停止运动.
如图,点A,点B在以点O为圆心的圆上,且∠AOB=30°,如果甲机器人从点A出发沿着圆周按顺时针方向以每秒5°的速度行驶,乙机器人从点B出发沿着圆周按逆时针方向行驶,速度是甲机器人的2倍,经过一段时间后,甲、乙分别运动到点C,点D,当乙机器人第一次到达点B时,甲、乙同时停止运动.(1)当射线OB是∠COD的角平分线时,求出∠AOC的度数.
(2)在机器人运动的整个过程中,若∠COD=90°,求甲机器人运动的时间(要求,在备用图中画出图形).
分析 (1)根据机器人的运动速度,设∠AOC=x°,则∠BOD=2x°,根据角平分线的定义,列出方程即可解答;
(2)根据运动过程中,∠COD=90°,可以分三种情况讨论,从而列出方程,解答即可.
解答 解:(1)甲机器人的运动速度每秒为5°,乙机器人的运动速度为每秒10°,
设∠AOC=x°,则∠BOD=2x°,
∵OB是∠COD的平分线,
∴∠BOC=∠BOD=x+30°,
∵∠BOD=2x°,
∴2x=30+x,解得:x=30°.
(2)分三种情况讨论:
①当OC,OD运动到如图1所示的位置时,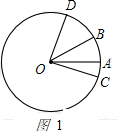
设甲的运动时间为t秒,则∠AOC=5t°,∠BOD=10t°,
∵∠COD=90°,∠AOB=30°,
∴5t+30+10t=90,解得:t=4;
②当OC,OD运动到如图2所示的位置时,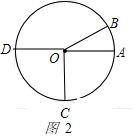
设甲的运动时间为t秒,则∠AOC=5t°,∠BOD=10t°,
∵∠COD=90°,∠AOB=30°,
∴5t+30+10t+90=360,解得:t=16;
③当OC,OD运动到如图3所示的位置时,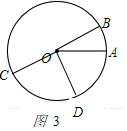
设甲的运动时间为t秒,则∠AOC=5t°,∠BOD=10t°,
∵∠COD=90°,∠AOB=30°,
∴5t+30+10t-90=360,解得:t=28;
答:在机器人运动的整个过程中,若∠COD=90°,甲运动的时间分别为4秒,16秒,28秒.
点评 本题主要考查角的运算中的动点问题及一元一次方程的应用,解决第(2)小题的关键是能考虑到各种满足∠COD的情况.

练习册系列答案
相关题目
10.用因式分解法把方程5m(m-3)=3-m分解成两个一次方程,正确的是( )
| A. | m-3=0,5m-1=0 | B. | 3-m=0,5m=0 | C. | 5m+1=0,m-3=0 | D. | 5m=0,m-3=0 |
15.在平面直角坐标系中,若点A(a,b)在第一象限内,则点B(a,-b)所在的象限( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
12.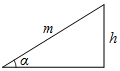 如图,某游乐场一山顶滑梯的高为h,滑梯的坡角为a,那么滑梯长m为( )
如图,某游乐场一山顶滑梯的高为h,滑梯的坡角为a,那么滑梯长m为( )
 如图,某游乐场一山顶滑梯的高为h,滑梯的坡角为a,那么滑梯长m为( )
如图,某游乐场一山顶滑梯的高为h,滑梯的坡角为a,那么滑梯长m为( )| A. | $\frac{h}{sinα}$ | B. | $\frac{h}{tanα}$ | C. | $\frac{h}{cosα}$ | D. | h-sinα |

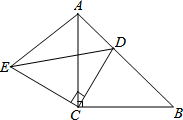 如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点,求证:
如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点,求证: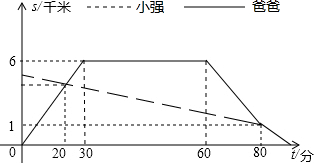 小强的爸爸从家骑自行车去图书馆借书,途中遇到了从图书馆步行回家的小强,爸爸借完书后迅速回家,途中追上了小强,便用自行车载上小强一起回家,结果爸爸比自己单独骑车回家晚到1分钟,两人与家的距离S(千米)和爸爸从家出发后的时间t(分钟)之间的关系如图所示.
小强的爸爸从家骑自行车去图书馆借书,途中遇到了从图书馆步行回家的小强,爸爸借完书后迅速回家,途中追上了小强,便用自行车载上小强一起回家,结果爸爸比自己单独骑车回家晚到1分钟,两人与家的距离S(千米)和爸爸从家出发后的时间t(分钟)之间的关系如图所示.