题目内容
1.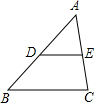 如图,在△ABC中,点D、E分别是AB、AC的中点,则下列结论:①BC=3DE;②△ADE∽△ABC;$③\frac{AD}{AE}=\frac{AB}{AC}$;④$\frac{三角形ADE面积}{四边形BCED的面积}=\frac{1}{3}$,其中正确的有( )
如图,在△ABC中,点D、E分别是AB、AC的中点,则下列结论:①BC=3DE;②△ADE∽△ABC;$③\frac{AD}{AE}=\frac{AB}{AC}$;④$\frac{三角形ADE面积}{四边形BCED的面积}=\frac{1}{3}$,其中正确的有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 先根据点DE分别是AB,AC的中点,得到DE是△ABC的中位线,进而得到BC=2DE,DE∥BC,据此得到△ADE∽△ABC,再根据相似三角形的性质进行判断即可.
解答 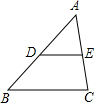 解:∵△ABC中,点DE分别是AB,AC的中点,
解:∵△ABC中,点DE分别是AB,AC的中点,
∴BC=2DE,DE∥BC,
∴△ADE∽△ABC,
∴$\frac{AD}{AB}$=$\frac{AE}{AC}$,即$\frac{AD}{AE}$=$\frac{AB}{AC}$,
∵$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=($\frac{DE}{BC}$)2=$\frac{1}{4}$,
∴$\frac{三角形ADE面积}{四边形BCED的面积}=\frac{1}{3}$,
故正确的有②,③,④.
故选:B.
点评 本题主要考查了三角形的中位线定理,相似三角形的性质和判定的应用,解决问题的关键是掌握:三角形的中位线平行于第三边,并且等于第三边的一半.解题时注意:相似三角形的面积之比等于相似比的平方.

练习册系列答案
 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
12.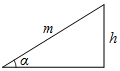 如图,某游乐场一山顶滑梯的高为h,滑梯的坡角为a,那么滑梯长m为( )
如图,某游乐场一山顶滑梯的高为h,滑梯的坡角为a,那么滑梯长m为( )
 如图,某游乐场一山顶滑梯的高为h,滑梯的坡角为a,那么滑梯长m为( )
如图,某游乐场一山顶滑梯的高为h,滑梯的坡角为a,那么滑梯长m为( )| A. | $\frac{h}{sinα}$ | B. | $\frac{h}{tanα}$ | C. | $\frac{h}{cosα}$ | D. | h-sinα |
6. 如图,△ABC≌△DEF,则∠C的度数是( )
如图,△ABC≌△DEF,则∠C的度数是( )
 如图,△ABC≌△DEF,则∠C的度数是( )
如图,△ABC≌△DEF,则∠C的度数是( )| A. | 56° | B. | 51° | C. | 107° | D. | 73° |
13.已知一个三位数A的百位数字是x,十位数字是y,个位数字是z,一个两位数B的十位数字是y,个位数字是x,则A-B的值是( )
| A. | 99x+z | B. | 99x-z | C. | 100x-y | D. | 99x+y |


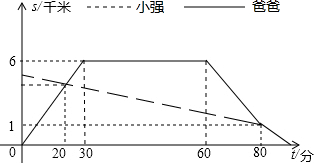 小强的爸爸从家骑自行车去图书馆借书,途中遇到了从图书馆步行回家的小强,爸爸借完书后迅速回家,途中追上了小强,便用自行车载上小强一起回家,结果爸爸比自己单独骑车回家晚到1分钟,两人与家的距离S(千米)和爸爸从家出发后的时间t(分钟)之间的关系如图所示.
小强的爸爸从家骑自行车去图书馆借书,途中遇到了从图书馆步行回家的小强,爸爸借完书后迅速回家,途中追上了小强,便用自行车载上小强一起回家,结果爸爸比自己单独骑车回家晚到1分钟,两人与家的距离S(千米)和爸爸从家出发后的时间t(分钟)之间的关系如图所示.