题目内容
5. 如图,边长为4个单位长度的正方形ABCD的边AB与等腰直角三角形EFG的斜边FG重合,△EFG以每秒1个单位长度的速度沿BC向右匀速运动(保持FG⊥BC),当点E运动到CD边上时△EFG停止运动,设△EFG的运动时间为t秒,△EFG与正方形ABCD重叠部分的面积为S,则S关于t的函数大致图象为( )
如图,边长为4个单位长度的正方形ABCD的边AB与等腰直角三角形EFG的斜边FG重合,△EFG以每秒1个单位长度的速度沿BC向右匀速运动(保持FG⊥BC),当点E运动到CD边上时△EFG停止运动,设△EFG的运动时间为t秒,△EFG与正方形ABCD重叠部分的面积为S,则S关于t的函数大致图象为( )| A. | 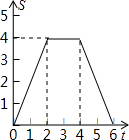 | B. | 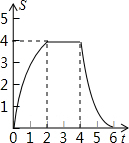 | C. | 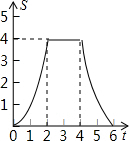 | D. | 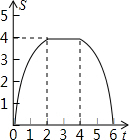 |
分析 根据题意可以求出各段对应的函数图象,从而可以判断哪个选项中的函数图象符合要求,本题得以解决.
解答 解:由题意可得,
FE=GE,AB=FG=4,∠FEG=90°,
则FE=GE=2$\sqrt{2}$,点E到FG的距离为2,
当点E从开始到点E到边BC上的过程中,S=$\frac{4×2}{2}-\frac{2(2-t)•(2-t)}{2}$=-t2+4t(0≤t≤2),
当点E从BC边上到边FG与DC重合时,S=$\frac{4×2}{2}=4$(2≤t≤4),
当边FG与DC重合到点E到边DC的过程中,S=$\frac{2[2-(t-4)]×[2-(t-4)]}{2}$=(6-t)2(4≤t≤6),
由上可得,选项B中函数图象符合要求,
故选B.
点评 本题考查动点问题的函数图象,解答此类问题的关键是明确题意,求出各段对应的函数图象,利用数形结合的思想解答.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
15.在平面直角坐标系中,若点A(a,b)在第一象限内,则点B(a,-b)所在的象限( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
13.已知一个三位数A的百位数字是x,十位数字是y,个位数字是z,一个两位数B的十位数字是y,个位数字是x,则A-B的值是( )
| A. | 99x+z | B. | 99x-z | C. | 100x-y | D. | 99x+y |
20.如果将“收入100元”记作“+100元”,那么“支出50元”应记作( )
| A. | +50元 | B. | -50元 | C. | +150元 | D. | -150元 |

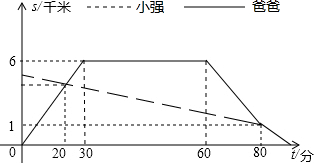 小强的爸爸从家骑自行车去图书馆借书,途中遇到了从图书馆步行回家的小强,爸爸借完书后迅速回家,途中追上了小强,便用自行车载上小强一起回家,结果爸爸比自己单独骑车回家晚到1分钟,两人与家的距离S(千米)和爸爸从家出发后的时间t(分钟)之间的关系如图所示.
小强的爸爸从家骑自行车去图书馆借书,途中遇到了从图书馆步行回家的小强,爸爸借完书后迅速回家,途中追上了小强,便用自行车载上小强一起回家,结果爸爸比自己单独骑车回家晚到1分钟,两人与家的距离S(千米)和爸爸从家出发后的时间t(分钟)之间的关系如图所示.