题目内容
已知∠AOB=60°,OC为∠AOB内部的一条射线,OM、ON分别平分∠AOC和∠BOC,则∠MON等于( )
| A、30° | B、90° |
| C、50° | D、40° |
考点:角平分线的定义
专题:
分析:根据角平分线的定义得到∠COM=
∠AOC,∠CON=
∠BOC,然后利用∠MON=∠COM+∠CON即可得到∠MON=
∠AOB,将∠AOB=60°代入计算即可.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答: 解:∵OM、ON分别平分∠AOC、∠BOC,
解:∵OM、ON分别平分∠AOC、∠BOC,
∴∠COM=
∠AOC,∠CON=
∠BOC,
∴∠MON=∠COM+∠CON=
(∠AOC+∠BOC)=
∠AOB,
∵∠AOB=60°,
∴∠MON=30°.
故选A.
 解:∵OM、ON分别平分∠AOC、∠BOC,
解:∵OM、ON分别平分∠AOC、∠BOC,∴∠COM=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠MON=∠COM+∠CON=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠AOB=60°,
∴∠MON=30°.
故选A.
点评:本题考查了角度的计算,角平分线的定义,比较简单.准确画出图形是解题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
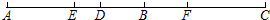 如图,点B、D在线段AC上,BD=
如图,点B、D在线段AC上,BD=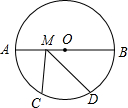 在⊙O中,AB是⊙O的直径,AB=8cm,
在⊙O中,AB是⊙O的直径,AB=8cm,
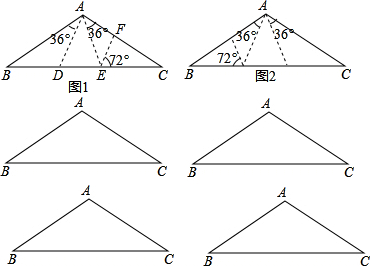 已知△ABC中AB=AC,∠BAC=108°,如图1,将它分割成四个非直角三角形,得其中的二个全等,二个相似(相似比不为1)请在以下四个图中设计不同的分割方法,将顶角为108°的等腰△ABC分割成四个非直角三角形,使得其中二个全等,另外二个相似(相似比不等于1),并在图上标注必要的角度,图1和图2被认为是同一种方法.
已知△ABC中AB=AC,∠BAC=108°,如图1,将它分割成四个非直角三角形,得其中的二个全等,二个相似(相似比不为1)请在以下四个图中设计不同的分割方法,将顶角为108°的等腰△ABC分割成四个非直角三角形,使得其中二个全等,另外二个相似(相似比不等于1),并在图上标注必要的角度,图1和图2被认为是同一种方法. 如图,已知线段AB,请用尺规按下列要求作图.
如图,已知线段AB,请用尺规按下列要求作图.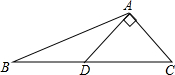 如图,在△ABC中,∠BAC=120°,AD⊥AC,D为BC中点,求tanC和cosC的值.
如图,在△ABC中,∠BAC=120°,AD⊥AC,D为BC中点,求tanC和cosC的值. 如图,已知A、B、C三点在⊙O上,AC⊥BO于D,∠B=53°,则∠BOC的度数是
如图,已知A、B、C三点在⊙O上,AC⊥BO于D,∠B=53°,则∠BOC的度数是