题目内容
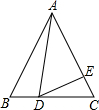如图，在边长为9的正三角形ABC中，BD=3，∠ADE=60°，则AE的长为（ ）| A、4 | B、5 | C、6 | D、7 |
考点：相似三角形的判定与性质,等边三角形的性质
专题：
分析：证明∠BAD=∠EDC，此为解决问题的关键性结论；证明△ABD∽△DCE，得到
=
，运用AB=9，BD=3，DC=6，求出CE，即可解决问题．
| AB |
| DC |
| BD |
| CE |
解答：解：∵△ABC是等边三角形，
∴∠B=∠C=60°，AB=BC=6；
∵∠ADE=60°，
∴∠BAD+∠ADB=∠ADB+∠EDC，
∴∠BAD=∠EDC，
∴△ABD∽△DCE，
∴
=
，而AB=9，BD=3，DC=6，
∴CE=2，AE=7，
故选D．
解：∵△ABC是等边三角形，∴∠B=∠C=60°，AB=BC=6；
∵∠ADE=60°，
∴∠BAD+∠ADB=∠ADB+∠EDC，
∴∠BAD=∠EDC，
∴△ABD∽△DCE，
∴
| AB |
| DC |
| BD |
| CE |
∴CE=2，AE=7，
故选D．
点评：该题主要考查了等边三角形的性质、相似三角形的判定及其性质等几何知识点及其应用问题；解题的关键是数形结合，准确掌握图形中隐含的数量关系．
练习册系列答案
相关题目
若A、O、B三点在同一条直线上，OA=3，OB=5，则A、B两点间的距离为（ ）
| A、2 | B、8 | C、3 | D、8或2 |
如图，点B、D在线段AC上，BD=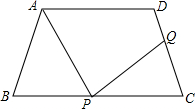
如图，在梯形ABCD中，∠ABC=∠DCB，AB=DC=6cm，BC=8cm，若点P从点B开始沿BC方向运动，同时点Q从点C开始沿CD方向运动，速度不一样，当它们的速度比是多少时，以A、B、P为顶点的三角形和以P、C、Q为顶点的三角形全等？
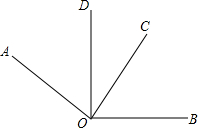如图，∠AOC和∠DOB都是直角，如果∠DOC=26°，那么∠AOB的度数是