题目内容
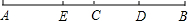 补全下列解题过程.
补全下列解题过程.如图,已知线段AB=12cm,点C为AB的中点,点D为BC的中点,在线段AC上取点E,使CE=
| 1 |
| 3 |
解:∵AB=12cm,点C为AB的中点,
∴AC=BC=
| 1 |
| 2 |
∵点D为BC的中点,
∴CD=
| 1 |
| 2 |
∵CE=
| 1 |
| 3 |
∴CE=
∴DE=CD+
考点:两点间的距离
专题:推理填空题
分析:根据线段中点的性质,可得AC,BC,CD的长,根据CE=
AC,可得CE的长,根据线段的和差,可得答案.
| 1 |
| 3 |
解答:解:∵AB=12cm,点C为AB的中点,
∴AC=BC=
AB=6cm
∵点D为BC的中点,
∴CD=
BC=3 cm.
∵CE=
AC,
∴CE=2 cm.
∴DE=CD+CE=5 cm.
∴AC=BC=
| 1 |
| 2 |
∵点D为BC的中点,
∴CD=
| 1 |
| 2 |
∵CE=
| 1 |
| 3 |
∴CE=2 cm.
∴DE=CD+CE=5 cm.
点评:本题考查了两点间的距离,利用了线段中点的性质,线段的和差.

练习册系列答案
相关题目
 C为等腰△ABE一腰AB延长线上一点且BC=EF,C,D,F三点共线,求证:CD=DF.
C为等腰△ABE一腰AB延长线上一点且BC=EF,C,D,F三点共线,求证:CD=DF.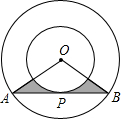 如图,两同心圆的圆心为O,半径分别为6,3,大圆的弦AB切小圆于P,则图中阴影部分的周长是
如图,两同心圆的圆心为O,半径分别为6,3,大圆的弦AB切小圆于P,则图中阴影部分的周长是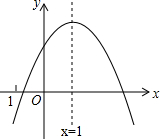 二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,下列结论中:①ac>0;②2a+b=0;③b2-4ac>0;④a-b+c>0.正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,下列结论中:①ac>0;②2a+b=0;③b2-4ac>0;④a-b+c>0.正确的是( )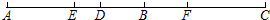 如图,点B、D在线段AC上,BD=
如图,点B、D在线段AC上,BD=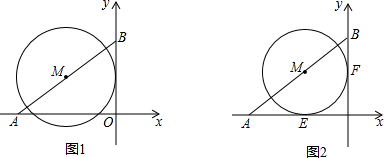
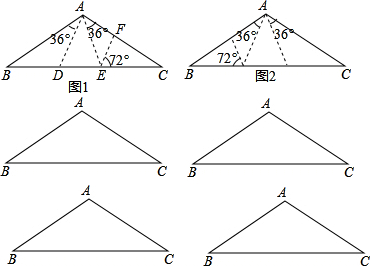 已知△ABC中AB=AC,∠BAC=108°,如图1,将它分割成四个非直角三角形,得其中的二个全等,二个相似(相似比不为1)请在以下四个图中设计不同的分割方法,将顶角为108°的等腰△ABC分割成四个非直角三角形,使得其中二个全等,另外二个相似(相似比不等于1),并在图上标注必要的角度,图1和图2被认为是同一种方法.
已知△ABC中AB=AC,∠BAC=108°,如图1,将它分割成四个非直角三角形,得其中的二个全等,二个相似(相似比不为1)请在以下四个图中设计不同的分割方法,将顶角为108°的等腰△ABC分割成四个非直角三角形,使得其中二个全等,另外二个相似(相似比不等于1),并在图上标注必要的角度,图1和图2被认为是同一种方法.