题目内容
如图，由四个全等的直角三角形及一个小正方形拼成一个大正方形，已知直角三角形的短直角边长为3，小正方形的面积为1，则大正方形的面积为考点：勾股定理的证明
专题：
分析：先求出直角三角形的短直角边长，可得直角三角形的长直角边长，即可得出直角三角形的斜边长，再利用正方形的面积公式求解即可．
解答：解：∵小正方形的面积为1，
∴小正方形的边长为1，
∵直角三角形的短直角边长为3，
∴直角三角形的长直角边长为3+1=4，
∴直角三角形的斜边长为
=5，
∴大正方形的面积为5×5=25．
故答案为：25．
∴小正方形的边长为1，
∵直角三角形的短直角边长为3，
∴直角三角形的长直角边长为3+1=4，
∴直角三角形的斜边长为
| 32+42 |
∴大正方形的面积为5×5=25．
故答案为：25．
点评：本题主要考查了勾股定理，解题的关键是熟记勾股定理．
练习册系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
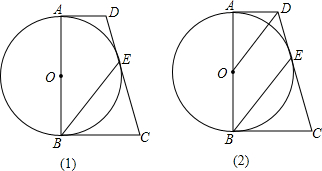
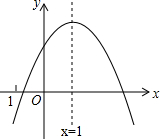二次函数y=ax2+bx+c（a≠0）的图象如图所示，其对称轴为x=1，下列结论中：①ac＞0；②2a+b=0；③b2-4ac＞0；④a-b+c＞0．正确的是（ ）
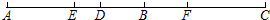如图，点B、D在线段AC上，BD=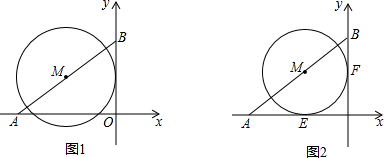
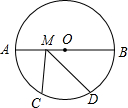在⊙O中，AB是⊙O的直径，AB=8cm，
如图，已知线段AB，请用尺规按下列要求作图．