题目内容
3.在每个小正方形的边长为1的网格中,点A,B在格点上.(Ⅰ)如图①,点C,D在格点上,线段CD与AB交于点P,则AP的值等于$\frac{2}{3}$$\sqrt{17}$;
(Ⅱ)请在如图②所示的网格中,用无刻度的直尺,在线段AB上画出一点P,使AP=$\frac{9}{25}$$\sqrt{17}$,并简要说明点P的位置是如何找到的(不要求证明)取格点C、D,连接CD,CD与AB交于点G,取格点F,两平行线的交点为E,连接EF,EF与AB交于点P,则点P即为所求.

分析 (1)利用格点,根据勾股定理求出AB的长,再根据相似三角形的性质得到AP的值;
(2)根据三角形相似,使得AG为AB长度的$\frac{3}{5}$;再根据三角形相似,使得AP为AG长度的$\frac{3}{5}$即可.
解答 解:(1)如图①,
AB=$\sqrt{{1}^{2}+{4}^{2}}$=$\sqrt{17}$,
AP=$\frac{2}{2+1}$AB=$\frac{2}{3}$$\sqrt{17}$;
(2)如图②所示:取格点C、D,连接CD,CD与AB交于点G,取格点F,两平行线的交点为E,连接EF,EF与AB交于点P,则点P即为所求.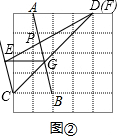
故答案为:$\frac{2}{3}$$\sqrt{17}$;取格点C、D,连接CD,CD与AB交于点G,取格点F,两平行线的交点为E,连接EF,EF与AB交于点P,则点P即为所求.
点评 本题考查了勾股定理,充分利用格点的特点和相似三角形的性质是解题的关键.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
13. 利用图中图形面积关系可以解释的公式是( )
利用图中图形面积关系可以解释的公式是( )
 利用图中图形面积关系可以解释的公式是( )
利用图中图形面积关系可以解释的公式是( )| A. | (a+b)2=a2+2ab+b2 | B. | (a-b)2=a2-2ab+b2 | ||
| C. | (a+b)(a-b)=a2-b2 | D. | (a+b)(a2-ab+b3)=a3+b3 |
18.甲仓库有水泥100吨,乙仓库有水泥80吨,要全部运动A、B两工地,已知A工地需要70吨,B工地需要110吨,甲仓库运到A、B两工地的运费分别是140元/吨、150元/吨,乙仓库运到A、B两工地的运费分别是200元/吨、80元/吨,本次运送水泥总运费需要25900元,问甲仓库运到A工地水泥的吨数.(运费:元/吨,表示运送每吨水泥所需的人民币)
(1)设甲仓库运到A工地水泥的吨数为x吨,请在下面表格中用x表示出其他未知量.
(2)用含x的代数式表示运送甲仓库100吨水泥的运费为-10x+15000元.(写出化简后的结果)
(3)请根据题目中的等量关系和以上的分析列出方程.(只列出方程即可,写成ax+b=0的形式,不用解)
(1)设甲仓库运到A工地水泥的吨数为x吨,请在下面表格中用x表示出其他未知量.
| 甲仓库 | 乙仓库 | |
| A工地 | x | 70-x |
| B工地 | 100-x | x+10 |
(3)请根据题目中的等量关系和以上的分析列出方程.(只列出方程即可,写成ax+b=0的形式,不用解)
 如图,以数轴的单位长度线段为边长作一个正方形,以表示数2的点为圆心,正方形对角线长为半径画半圆,交数轴于点A和点B,则点A表示的数是2-$\sqrt{2}$.
如图,以数轴的单位长度线段为边长作一个正方形,以表示数2的点为圆心,正方形对角线长为半径画半圆,交数轴于点A和点B,则点A表示的数是2-$\sqrt{2}$. 如图,在数轴上的点A、点B之间表示整数的点有4个.
如图,在数轴上的点A、点B之间表示整数的点有4个. 如图,平移所给图形,使点A移动到点A1.
如图,平移所给图形,使点A移动到点A1.