题目内容
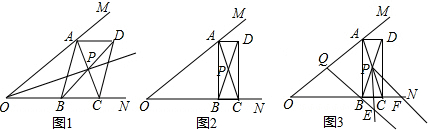
20．
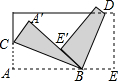将一长方形纸片，按图中的方式折叠，BC、BD为折痕，折叠后点E′刚好落在A′B上，则∠CBD的度数为（ ）| A． | 60° | B． | 75° | C． | 90° | D． | 95° |
分析 由折叠的性质可知，∠ABC=∠A′BC，∠EBD=∠E′BD，根据平角=180°结合∠CBD=∠CBA′+∠E′BD，即可得出2∠CBD=180°，进而即可得出∠CBD=90°，此题得解．
解答 解：根据折叠的性质可知：∠ABC=∠A′BC，∠EBD=∠E′BD，
∵∠ABC+∠A′BC+∠E′BD+∠EBD=180°，∠CBD=∠CBA′+∠E′BD，
∴2∠CBD=180°，
∴∠CBD=90°．
故选C．
点评 本题考查了角的计算以及翻折变换，根据角的计算结合平角为180°找出2∠CBD=180°是解题的关键．
练习册系列答案
小题狂做系列答案
相关题目
5．下列等式成立的是（ ）
| A． | $\frac{2}{a}$+$\frac{3}{b}$=$\frac{5}{ab}$ | B． | $\frac{3}{3a+b}$=$\frac{1}{a+b}$ | C． | $\frac{ab}{ab-{b}^{2}}$=$\frac{a}{a-b}$ | D． | $\frac{a}{-a+b}$=-$\frac{a}{a+b}$ |
在平面直角坐标中，抛物线y=ax2+bx+3与x轴分别交于点A（2，0）、点B（点B在点A右侧），与y轴交于点C，tan∠CBA=$\frac{1}{2}$．