题目内容
10. 在平面直角坐标中,抛物线y=ax2+bx+3与x轴分别交于点A(2,0)、点B(点B在点A右侧),与y轴交于点C,tan∠CBA=$\frac{1}{2}$.
在平面直角坐标中,抛物线y=ax2+bx+3与x轴分别交于点A(2,0)、点B(点B在点A右侧),与y轴交于点C,tan∠CBA=$\frac{1}{2}$.(1)求抛物线的表达式;
(2)将(1)中抛物线向下平移m个单位,点A、B、C平移后的位置分别为点A1、B1、C1,若点D(10,5)满足∠C1B1D=90°,求平移后抛物线的解析式.
分析 (1)求出A、B、C三点坐标即可解决问题.
(2)如图作DG⊥A1B1于G,延长B1A1交y轴于E.由△EB1C1∽△GDB1,可得$\frac{E{C}_{1}}{G{B}_{1}}$=$\frac{E{B}_{1}}{DG}$,即$\frac{3}{4}$=$\frac{6}{DG}$,推出DG=8,推出B1(6,-3),推出原来抛物线向下平移3个即可得到新的抛物线,延长即可解决问题.
解答 解:(1)∵C(0,3),
∴OC=3,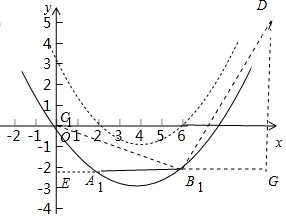
∵tan∠CBA=$\frac{1}{2}$,
∴OB=6,
∵A(2,0),B在A右边,
∴B(6,0),
设抛物线的解析式为y=a(x-2)(x-6),把(0,3)代入得到a=$\frac{1}{4}$,
∴y=$\frac{1}{4}$x2-2x+3.
(2)如图作DG⊥A1B1于G,延长B1A1交y轴于E.
∵∠C1B1G=90°,
∴△EB1C1∽△GDB1,
∴$\frac{E{C}_{1}}{G{B}_{1}}$=$\frac{E{B}_{1}}{DG}$,
∴$\frac{3}{4}$=$\frac{6}{DG}$,
∴DG=8,
∴B1(6,-3),
∴原来抛物线向下平移3个即可得到新的抛物线,
∴新的抛物线的解析式为y=$\frac{1}{4}$x2-2x.
点评 本题考查抛物线与x轴的交点、平移变换、相似三角形的判定和性质、锐角三角函数等知识,解题的关键是熟练掌握待定系数法确定函数解析式,学会添加常用辅助线,构造相似三角形解决问题,属于中考常考题型.

练习册系列答案
相关题目
20.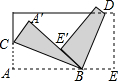 将一长方形纸片,按图中的方式折叠,BC、BD为折痕,折叠后点E′刚好落在A′B上,则∠CBD的度数为( )
将一长方形纸片,按图中的方式折叠,BC、BD为折痕,折叠后点E′刚好落在A′B上,则∠CBD的度数为( )
 将一长方形纸片,按图中的方式折叠,BC、BD为折痕,折叠后点E′刚好落在A′B上,则∠CBD的度数为( )
将一长方形纸片,按图中的方式折叠,BC、BD为折痕,折叠后点E′刚好落在A′B上,则∠CBD的度数为( )| A. | 60° | B. | 75° | C. | 90° | D. | 95° |
15.下列等式由左边至右边的变形中,属于因式分解的是( )
| A. | x2+3x-1=x(x+3)-1 | B. | x2-9+2x=(x+3)(x-3)+2x | ||
| C. | a2-16=(a+4)(a-4) | D. | (x+2)(x-2)=x2-4 |
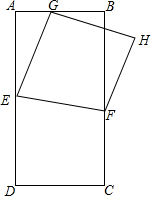 矩形ABCD满足BC=2AB,E、F分别为AD、BC边上的动点,连接EF,沿EF将四边形DEFC翻折至四边形GEFH,点G落在AB上.
矩形ABCD满足BC=2AB,E、F分别为AD、BC边上的动点,连接EF,沿EF将四边形DEFC翻折至四边形GEFH,点G落在AB上.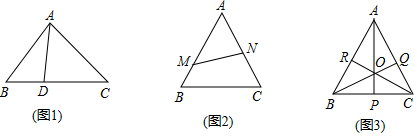
 如图,BD是△ABC的中线,点E、F分别为BD、CE的中点,若△AEF的面积为3cm2,则△ABC的面积是12cm2.
如图,BD是△ABC的中线,点E、F分别为BD、CE的中点,若△AEF的面积为3cm2,则△ABC的面积是12cm2.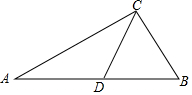 如图,在△ABC中,CD是边AB上的中线,∠B是锐角,且sinB=$\frac{\sqrt{2}}{2}$,tanA=$\frac{1}{2}$,AC=3$\sqrt{5}$
如图,在△ABC中,CD是边AB上的中线,∠B是锐角,且sinB=$\frac{\sqrt{2}}{2}$,tanA=$\frac{1}{2}$,AC=3$\sqrt{5}$