题目内容
8.如图①,点A、B分别在射线OM,ON上,且∠MON为钝角,现以线段OA、OB为斜边向∠MON的外侧作等腰直角三角形,分别是△OAP和△OBQ,点C、D分别是OA、OB的中点,且四边形CODE是平行四边形.(1)求证:△PCE≌△EDQ;
(2)如图②,延长PC,QD交于点R.若∠MON=150°,求证:△ABR为等边三角形.
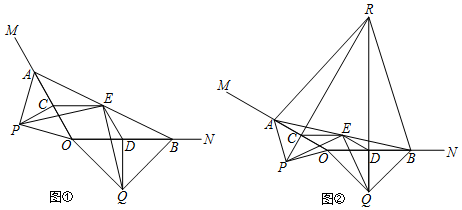
分析 (1)根据等腰直角三角形的性质、平行四边形的性质得到∠PCE=∠EDQ,根据边角边公理证明即可;
(2)连结RO,根据线段垂直平分线的判定定理和性质定理得到AR=OR=BR,根据等边三角形的判定定理证明即可.
解答 (1)证明:∵△OAP是等腰直角三角形,且点C是OA的中点,
∴△PCA和△PCO都是等腰直角三角形,
∴PC=AC=OC,∠PCO=90°,
同理:QD=OD=BD,∠QDO=90°,
∵四边形CODE是平行四边形,
∴CE=OD,ED=OC,
∴ED=PC,QD=CE,
∵CE∥ON,DE∥OM,
∴∠ACE=∠AOD,∠BDE=∠AOD,
∴∠ACE=∠BDE,
∴∠OCE=∠ODE,
∴∠OCE+∠PCO=∠ODE+∠QDO,
即∠PCE=∠EDQ,
在△PCE与△EDQ中,
$\left\{\begin{array}{l}PC=ED\\∠PCE=∠EDQ\\ CE=DQ\end{array}\right.$,
∴△PCE≌△EDQ;
(2)连结RO,
∵△OAP和△OBQ均为等腰直角三角形,点C、D分别是OA、OB的中点,
∴PR与QR分别是OA,OB的垂直平分线,
∴AR=OR=BR,
∴∠ARC=∠ORC,∠ORD=∠BRD,
∵∠RCO=∠RDO=90°,∠COD=150°,
∴∠CRD=30°,
∴∠ARB=60°,
∴△ARB是等边三角形.
点评 本题考查的是等腰直角三角形的性质、平行四边形的性质、全等三角形的判定和性质,掌握等腰直角三角形的性质、等边三角形的判定定理是解题的关键.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
19.二次函数y=x2-2的图象的顶点是( )
| A. | (2,-2) | B. | (-1,0) | C. | (1,9) | D. | (0,-2) |
16. 如右图所示的工件的主视图是( )
如右图所示的工件的主视图是( )
 如右图所示的工件的主视图是( )
如右图所示的工件的主视图是( )| A. |  | B. |  | C. |  | D. |  |
20.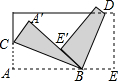 将一长方形纸片,按图中的方式折叠,BC、BD为折痕,折叠后点E′刚好落在A′B上,则∠CBD的度数为( )
将一长方形纸片,按图中的方式折叠,BC、BD为折痕,折叠后点E′刚好落在A′B上,则∠CBD的度数为( )
 将一长方形纸片,按图中的方式折叠,BC、BD为折痕,折叠后点E′刚好落在A′B上,则∠CBD的度数为( )
将一长方形纸片,按图中的方式折叠,BC、BD为折痕,折叠后点E′刚好落在A′B上,则∠CBD的度数为( )| A. | 60° | B. | 75° | C. | 90° | D. | 95° |
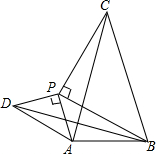 如图,已知线段AB=2,点P是线段AB外的一个动点,且PA=1,以PA,PB为腰向外作等腰直角三角形PAD和等腰直角三角形PBC,连结AC,BD.
如图,已知线段AB=2,点P是线段AB外的一个动点,且PA=1,以PA,PB为腰向外作等腰直角三角形PAD和等腰直角三角形PBC,连结AC,BD. 若⊙O是等边△ABC的外接圆,⊙O的半径为2,则等边△ABC的边长为$2\sqrt{3}$.
若⊙O是等边△ABC的外接圆,⊙O的半径为2,则等边△ABC的边长为$2\sqrt{3}$.