题目内容
11.阅读下面材料:在数学课上,老师请同学思考如下问题:如图1,我们把一个四边形ABCD的四边中点E,F,G,H依次连接起来得到的四边形EFGH是平行四边形吗?小敏在思考问题是,有如下思路:连接AC.
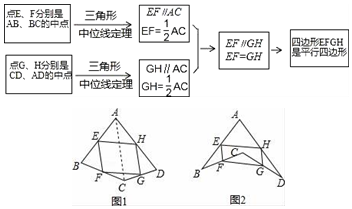
结合小敏的思路作答
(1)若只改变图1中四边形ABCD的形状(如图2),则四边形EFGH还是平行四边形吗?说明理由;参考小敏思考问题方法解决一下问题:
(2)如图2,在(1)的条件下,若连接AC,BD.当AC与BD满足什么条件时,四边形EFGH是矩形,直接写出结论.
分析 (1)如图2,连接AC,根据三角形中位线的性质得到EF∥AC,EF=$\frac{1}{2}$AC,然后根据平行四边形判定定理即可得到结论;
(2)根据平行线的性质得到GH⊥BD,GH⊥GF,于是得到∠HGF=90°,根据矩形的判定定理即可得到结论.
解答 解:(1)是平行四边形, 理由如下:
理由如下:
如图2,连接AC,
∵E是AB的中点,F是BC的中点,
∴EF∥AC,EF=$\frac{1}{2}$AC,
同理HG∥AC,HG=$\frac{1}{2}$AC,
综上可得:EF∥HG,EF=HG,
故四边形EFGH是平行四边形;
(2)当AC⊥BD时,四边形EFGH为矩形;
理由如下:
同(1)得:四边形EFGH是平行四边形,
∵AC⊥BD,GH∥AC,
∴GH⊥BD,
∵GF∥BD,
∴GH⊥GF,
∴∠HGF=90°,
∴四边形EFGH为矩形.
点评 此题主要考查了中点四边形,关键是掌握三角形中位线定理,三角形的中位线平行于第三边且等于第三边的一半.

练习册系列答案
相关题目
12.云南高铁自开通以来,发展速度不断加快,现已成为云南市民主要出行方式之一.今年五一期间安全运输乘客约5460000人次.用科学记数法表示5460000为( )
| A. | 5.46×107 | B. | 5.46×106 | C. | 5.5×106 | D. | 546×104 |
19.二次函数y=x2-2的图象的顶点是( )
| A. | (2,-2) | B. | (-1,0) | C. | (1,9) | D. | (0,-2) |
16. 如右图所示的工件的主视图是( )
如右图所示的工件的主视图是( )
 如右图所示的工件的主视图是( )
如右图所示的工件的主视图是( )| A. |  | B. |  | C. |  | D. |  |
20.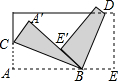 将一长方形纸片,按图中的方式折叠,BC、BD为折痕,折叠后点E′刚好落在A′B上,则∠CBD的度数为( )
将一长方形纸片,按图中的方式折叠,BC、BD为折痕,折叠后点E′刚好落在A′B上,则∠CBD的度数为( )
 将一长方形纸片,按图中的方式折叠,BC、BD为折痕,折叠后点E′刚好落在A′B上,则∠CBD的度数为( )
将一长方形纸片,按图中的方式折叠,BC、BD为折痕,折叠后点E′刚好落在A′B上,则∠CBD的度数为( )| A. | 60° | B. | 75° | C. | 90° | D. | 95° |
 如图,已知∠1=60°,∠2=120°,∠BAC=50°,求∠C的度数.
如图,已知∠1=60°,∠2=120°,∠BAC=50°,求∠C的度数.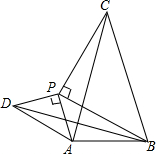 如图,已知线段AB=2,点P是线段AB外的一个动点,且PA=1,以PA,PB为腰向外作等腰直角三角形PAD和等腰直角三角形PBC,连结AC,BD.
如图,已知线段AB=2,点P是线段AB外的一个动点,且PA=1,以PA,PB为腰向外作等腰直角三角形PAD和等腰直角三角形PBC,连结AC,BD.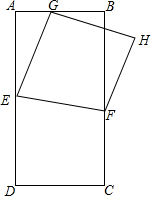 矩形ABCD满足BC=2AB,E、F分别为AD、BC边上的动点,连接EF,沿EF将四边形DEFC翻折至四边形GEFH,点G落在AB上.
矩形ABCD满足BC=2AB,E、F分别为AD、BC边上的动点,连接EF,沿EF将四边形DEFC翻折至四边形GEFH,点G落在AB上.