题目内容
开口向下的抛物线y＝(m2－2)x2＋2mx＋1的对称轴经过点(－1，3)，则m＝_____．
－1
【解析】由于抛物线y=（m2-2）x2+2mx+1的对称轴经过点（-1，3），
∴对称轴为直线x=-1，x==-1，
解得m1=-1，m2=2．
由于抛物线的开口向下，所以当m=2时，m2-2=2＞0，不合题意，应舍去，
∴m=-1．
故答案为：-1.
阳光课堂课时作业系列答案
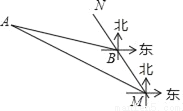
鹰派教辅衔接教材河北教育出版社系列答案如图，MN表示某引水工程的一段设计路线，从点M到点N的走向为北偏西30°，在点M的北偏西60°方向上有一点A，以点A为圆心，以500米为半径的圆形区域为居民区，取MN上另一点B，测得BA的方向为北偏西75°．已知MB=400米，若不改变方向，则输水路线是否会穿过居民区？请通过计算说明理由．（参考数据：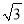 
≈1.732）
不会穿过居民区，理由见解析.
【解析】试题分析：要判断输水路线是否会穿过居民区，即要比较点A到MN的距离与500的大小，要求点A到MN的距离，作AD⊥MN交MN于点D，设AD=x，不难表示出DM=x+400，再由tan∠AMD==列出方程，解出x，比较x与500的大小，若x＞500，则不会穿过居民区；若x≤500，则会穿过居民区.
试题解析：
【解析】
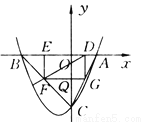
过A作AD⊥MN于点D，... 如图所示，已知抛物线P：y＝ax2＋bx＋c(a≠0)与x轴交于A，B两点(点A在x轴的正半轴上)，与y轴交于点C，矩形DEFG的一条边DE在线段AB上，顶点F，G分别在线段BC，AC上，抛物线P上的部分点的横坐标对应的纵坐标如下.
(1)求A，B，C三点的坐标；
(2)若点D的坐标为(m，0)，矩形DEFG的面积为S，求S与m的函数关系式，并指出m的取值范围；
(3)当矩形DEFG的面积S最大时，连接DF并延长至点M，使FM＝k·DF，若点M不在抛物线P上，求k的取值范围；
(4)若点D的坐标为(1，0)，求矩形DEFG的面积．
（1）A(2，0)，B(－4，0)，C(0，－4)；（2）S矩形DEFG=12m－6m2(0＜m＜2)；（3）k的取值范围是k≠且k＞0；（4）S矩形DEFG＝6．
【解析】试题分析：（1）可任选三组坐标，用待定系数法即可求出抛物线P的解析式．然后根据抛物线P的解析式即可得出A、B、C三点的坐标；
（2）求矩形的面积需知道矩形的长和宽，可先在直角三角形AOC中，根据AD，OA，DG，C... 在二次函数y＝ax2＋bx＋c中，若a与c异号，则其图象与x轴的交点个数为( )
A. 2个 B. 1个 C. 0个 D. 不能确定
A
【解析】【解析】
∵a与c异号，∴ac＜0，∴△=＞0，∴二次函数图象与x轴的交点个数为2．故选A． 已知函数y＝mx2－6x＋1(m是常数)．
(1)求证：不论m为何值，该函数的图象都经过y轴上的一个定点；
(2)若该函数的图象与x轴只有一个交点，求m的值．
（1）证明见解析；（2）m的值为0或9.
【解析】试题分析：（1）根据解析式可知，当x=0时，与m值无关，故可知不论m为何值，函数y= ﹣6x+1的图象都经过y轴上一个定点（0，1）．
（2）应分两种情况讨论：①当函数为一次函数时，与x轴有一个交点；
②当函数为二次函数时，利用根与系数的关系解答．
试题解析：（1）当x=0时，y=1．
所以不论m为何值，函数y= ﹣6... 如图，对称轴平行于y轴的抛物线与x轴交于(1，0)、(3，0)两点，则它的对称轴为____________________．
直线x＝2
【解析】试题分析：当两点到对称轴距离相等时，则所对应的函数值相等，则二次函数的对称轴为：x==2. 已知抛物线y＝x2－2x＋m＋1与x轴有两个不同的交点，则函数y＝
的大致图象是( )
A. （A） B. （B） C. （C） D. （D）
A
【解析】抛物线y=x2-2x+m+1与x轴有两个不同的交点，可得△=（-2）2-4（m+1）＞0，解得m＜0，因此可得函数y=的图象位于二、四象限，
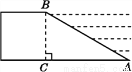
故选：A． 拦水坝横断面如图所示,迎水坡AB的坡比是1∶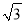
,坝高BC=10 m,则坡面AB的长度是( )
A. 15 m B. 20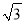
m C. 10
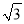m D. 20 m
D
【解析】在Rt△ABC中，BC＝10m， ，∴ (m)，
∴．故选D． 观察下列各式：①2a＋b和a＋b，②5m（a－b）和－a＋b，③3（a＋b）和－a－b，④x2－y2和x2+y2。其中有公因式的是（ ）
A．①② B.②③ C．③④ D．①④
B
【解析】
试题分析：根据公因式的定义依次分析各小题即可判断.
①2a＋b和a＋b，④x2－y2和x2+y2，没有公因式；
②5m（a－b）和－a＋b=－（a－b），公因式为a－b，③3（a＋b）和－a－b=－（a＋b），公因式为a+b，
故选B.