题目内容
在体育测试时，初三的一名高个子男生推铅球，已知铅球所经过的路线是某二次函数图象的一部分(如图)，若这个男生出手处A点的坐标为(0，2)，铅球路线的最高处B点的坐标为B(6，5).
(1)求这个二次函数的表达式；
(2)该男生把铅球推出去多远?(精确到0.01米).
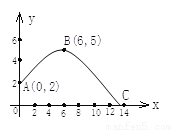
（1）y= (x-6)2+5；（2）该男生把铅球推出约13.75米
【解析】试题分析：（1）根据顶点坐标B(6,5)可设函数关系式为y=a(x-6)2+5，再把A(0,2)代入即可求得结果；
（2）把y=0代入求得图象与x轴的交点坐标，即可得到结果.
(1)设y=a(x-6)2+5,
则由A(0,2)得2=a(0-6)2+5，解得a=.
故y= (x-6)2+5；
...
课课练江苏系列答案
名牌中学课时作业系列答案
明天教育课时特训系列答案有两条或两条以上对称轴的轴对称图形是（ ）
A. 等腰三角形 B. 角 C. 等边三角形 D. 锐角三角形
C
【解析】A.等腰三角形只有一条对称轴；
B.角也只有一条对称轴，是角平分线所在的直线；
C.等边三角形有三条对称轴；
D.锐角三角形的对称轴数量不确定.
故选：C 某工厂在生产过程中要消耗大量电能，消耗每千度电产生利润与电价是一次函数关系，经过测算，工厂每千度电产生利润y（元/千度））与电价x（元/千度）的函数图象如图：
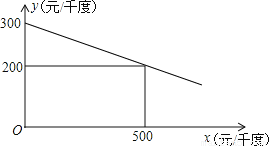
（1）当电价为600元/千度时，工厂消耗每千度电产生利润是多少？
（2）为了实现节能减排目标，有关部门规定，该厂电价x（元/千度）与每天用电量m（千度）的函数关系为x=10m+500，且该工厂每天用电量不超过60千度，为了获得最大利润，工厂每天应安排使用多少度电？工厂每天消耗电产生利润最大是多少元？
（1）工厂消耗每千度电产生利润是180元（2）当工厂每天消耗50千度电时，工厂每天消耗电产生利润为5000元
【解析】试题分析：（1）设y=kx+b（k≠0），利用待定系数法求一次函数解析式解答即可；
（2）根据利润=每天的用电量×每千度电产生利润y，然后整理得到W与m的关系式，再根据二次函数的最值问题解答．
【解析】
（1）设工厂每千度电产生利润y（元/千度）与电价x（元/千... 如图，二次函数y= -x2-2x的图象与x轴交于点A、O，在抛物线上有一点P，满足
S△AOP=3，则点P的坐标是（ ）
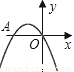
A. （-3，-3） B. （1，-3） C. （-3，-3）或（-3，1） D. （-3，-3）或（1，-3）
D
【解析】分析：根据抛物线的解析式，即可确定点A的坐标，由于OA是定长，根据△AOP的面积即可确定P点纵坐标的绝对值，将其代入抛物线的解析式中，即可求得P点的坐标．
解答：【解析】
抛物线的解析式中，令y=0，得：-x2-2x=0，解得x=0，x=-2；
∴A（-2，0），OA=2；
∵S△AOP=OA?|yP|=3，∴|yP|=3；
当P点纵坐标为3时，-x2-... 如图所示，已知抛物线P：y＝ax2＋bx＋c(a≠0)与x轴交于A，B两点(点A在x轴的正半轴上)，与y轴交于点C，矩形DEFG的一条边DE在线段AB上，顶点F，G分别在线段BC，AC上，抛物线P上的部分点的横坐标对应的纵坐标如下.
(1)求A，B，C三点的坐标；
(2)若点D的坐标为(m，0)，矩形DEFG的面积为S，求S与m的函数关系式，并指出m的取值范围；
(3)当矩形DEFG的面积S最大时，连接DF并延长至点M，使FM＝k·DF，若点M不在抛物线P上，求k的取值范围；
(4)若点D的坐标为(1，0)，求矩形DEFG的面积．
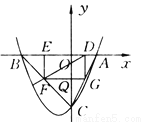
（1）A(2，0)，B(－4，0)，C(0，－4)；（2）S矩形DEFG=12m－6m2(0＜m＜2)；（3）k的取值范围是k≠且k＞0；（4）S矩形DEFG＝6．
【解析】试题分析：（1）可任选三组坐标，用待定系数法即可求出抛物线P的解析式．然后根据抛物线P的解析式即可得出A、B、C三点的坐标；
（2）求矩形的面积需知道矩形的长和宽，可先在直角三角形AOC中，根据AD，OA，DG，C... 若抛物线y=kx2－2x＋l与x轴有两个交点，则k的取值范围是____．
k＜1，且k≠0
【解析】【解析】
∵y=kx2﹣2x+1为二次函数，∴k≠0．
∵抛物线y=kx2﹣2x+1的图象与x轴有两个交点，∴△＞0，即（﹣2）2－4k＞0．
解得：k＜1，∴k的取值范围是k＜1且k≠0．
故答案为：k＜1且k≠0． 在二次函数y＝ax2＋bx＋c中，若a与c异号，则其图象与x轴的交点个数为( )
A. 2个 B. 1个 C. 0个 D. 不能确定
A
【解析】【解析】
∵a与c异号，∴ac＜0，∴△=＞0，∴二次函数图象与x轴的交点个数为2．故选A． 如图，对称轴平行于y轴的抛物线与x轴交于(1，0)、(3，0)两点，则它的对称轴为____________________．
直线x＝2
【解析】试题分析：当两点到对称轴距离相等时，则所对应的函数值相等，则二次函数的对称轴为：x==2. 如果水流的速度为a m/min(定量)，那么每分钟的进水量Q(m3)与所选择的水管直径D(m)之间的函数关系式是什么?
Q＝.
【解析】试题分析：根据圆柱体的体积公式V=πr2h，直接代入求解即可.
试题解析：函数关系式为Q＝a·π·()2＝ .