题目内容
如图，有一块含有45°角的直角三角板的两个锐角顶点放在直尺的对边上．如果∠1=22°，那么∠2的度数是考点：平行线的性质
专题：
分析：先根据直角三角板的性质得出∠BAC度数，故可得出∠BAC+∠1的度数，由平行线的性质即可得出结论．
解答：
解：∵图中是一块含有45°角的直角三角板，
∴∠BAC=45°．
∵∠1=22°，
∴∠BAC+∠1=45°+22°=67°．
∵直尺的两边互相平行，
∴∠2=∠BAC+∠1=67°．
故答案为：67°．
解：∵图中是一块含有45°角的直角三角板，∴∠BAC=45°．
∵∠1=22°，
∴∠BAC+∠1=45°+22°=67°．
∵直尺的两边互相平行，
∴∠2=∠BAC+∠1=67°．
故答案为：67°．
点评：本题考查的是平行线的性质，用到的知识点为：两直线平行，同位角相等．
练习册系列答案
相关题目
反比例函数y=
（m≠3）在图象所在的每一象限内，函数值y随自变量x的增大而增大，则m的取值范围是（ ）
| m-3 |
| x |
| A、m＞3 | B、m＜3 |
| C、m＞-3 | D、m＜-3 |
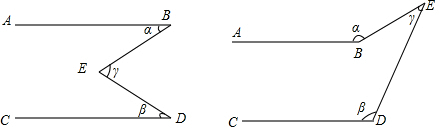
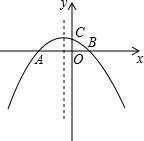如图，抛物线y=-