题目内容
16.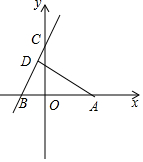 如图,在直角坐标系xOy中,点A(2,0)和点B(-2,0),直线BC与y轴正半轴交于点C(0,b),过点A作AD⊥BC,垂足为D,联结OD.
如图,在直角坐标系xOy中,点A(2,0)和点B(-2,0),直线BC与y轴正半轴交于点C(0,b),过点A作AD⊥BC,垂足为D,联结OD.(1)求OD的长;
(2)当∠ODA=30°时,求点C的坐标;
(3)在(2)的条件下,已知点E在直角坐标平面内,如果以A、C、D、E为顶点的四边形是平行四边形,请直接写出点E的坐标.
分析 (1)根据直角三角形斜边中线等于斜边一半,即可解决问题.
(2)首先证明∠CBO=60°,在Rt△OBC中,根据OC=OB•tan60°计算即可.
(3)点E有三种可能,利用平行四边形的性质,以及中点坐标公式即可解决问题.
解答 解:(1)如图,∵AD⊥BC,
∴∠ADB=90°,
∵A(2,0),B(-2,0),
∴OA=OB=2,
∴OD=$\frac{1}{2}$AB=2.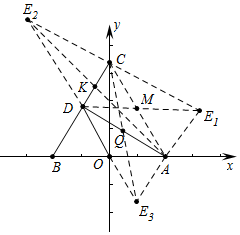
(2)∵∠ODA=30°,OD=OA,
∴∠ODA=∠OAD=30°,
∴∠OBD=60°,
在Rt△OBC中,OC=OB•tan60°=2$\sqrt{3}$,
∴C(0,2$\sqrt{3}$).
(3)∵四边形ADCE1是平行四边形,∴CM=AM,DM=ME1,
∵C(0,2$\sqrt{3}$),A(2,0),
∴M(1,$\sqrt{3}$),
∴E1(3,$\sqrt{3}$),同法可得E2(-3,3$\sqrt{3}$),E3(1,-$\sqrt{3}$).
点评 本题考查平行四边形的判定、坐标与图形的性质、锐角三角函数、直角三角形斜边中线定理、中点坐标公式等知识,解题的关键是灵活运用所学知识解决问题,考虑问题要全面,不能漏解,属于中考常考题型.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
7. 已知:AB∥CD,∠1=80°,∠2=50°,则∠ADC等于( )
已知:AB∥CD,∠1=80°,∠2=50°,则∠ADC等于( )
 已知:AB∥CD,∠1=80°,∠2=50°,则∠ADC等于( )
已知:AB∥CD,∠1=80°,∠2=50°,则∠ADC等于( )| A. | 110° | B. | 120° | C. | 130° | D. | 140° |
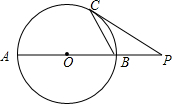 如图,在⊙O中,AB为直径,C为⊙O上一点,过点C作⊙O的切线,与AB的延长线相交于点P,若∠CAB=27°,求∠P的大小.
如图,在⊙O中,AB为直径,C为⊙O上一点,过点C作⊙O的切线,与AB的延长线相交于点P,若∠CAB=27°,求∠P的大小.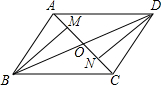 如图,?ABCD的对角线AC,BD相交于点O,M,N分别是OA,OC的中点,求证:BM∥DN,且BM=DN.
如图,?ABCD的对角线AC,BD相交于点O,M,N分别是OA,OC的中点,求证:BM∥DN,且BM=DN.