题目内容
3.某城市规定:出租车起步价行驶的是最远路程为3千米,越过3千米的部分按每千米另外收费,甲说:“我乘这种出租车行驶了11千米,付了17元”;乙说:“我乘这种出租车行驶了23千米,付了35元”.(1)请你算一算这种出租车的起步价是多少元?以及超过3千米后,每千米的车费是多少元?
(2)若丙乘这种出租车从A地到B地,至少需要50元钱,问A地到B地的距离至少是多少千米?
分析 (1)设起步价为x元,超过3千米后每千米的车费是y元,根据不同的路程的付费不同,可得方程组,根据解方程组,可得答案;
(2)设A地到B地的距离至少是a千米,根据从A地到B地至少需要50元钱,列出不等式,进行求解即可.
解答 解:(1)设起步价为x元,超过3千米后每千米的车费是y元,由题意,得
$\left\{\begin{array}{l}{x+(11-3)y=17}\\{x+(23-3)y=35}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=5}\\{y=1.5}\end{array}\right.$,
答:这种出租车的起步价是3元,以及超过3千米后,每千米的车费是1.5元;
(2)设A地到B地的距离至少是a千米,根据题意得:
5+(a-3)×1.5≥50,
解得:a≥33,
答:A地到B地的距离至少是33千米.
点评 此题考查了二元一次方程组和一元一次不等式的应用,解决问题的关键是读懂题意,找到关键描述语,找到所求的量的数量关系,列出方程组和不等式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18. 如图,AB、CD相交于O,OE⊥AB,那么下列结论错误的是( )
如图,AB、CD相交于O,OE⊥AB,那么下列结论错误的是( )
 如图,AB、CD相交于O,OE⊥AB,那么下列结论错误的是( )
如图,AB、CD相交于O,OE⊥AB,那么下列结论错误的是( )| A. | ∠AOC与∠BOD是对顶角 | B. | ∠AOC与∠COE互为余角 | ||
| C. | ∠BOD与∠COE互为余角 | D. | ∠COE与∠BOE互为补角 |
8. 如图,已知ED∥BC,DF∥AB,∠B=∠C,图中与∠DFC相等的角有( )个.
如图,已知ED∥BC,DF∥AB,∠B=∠C,图中与∠DFC相等的角有( )个.
 如图,已知ED∥BC,DF∥AB,∠B=∠C,图中与∠DFC相等的角有( )个.
如图,已知ED∥BC,DF∥AB,∠B=∠C,图中与∠DFC相等的角有( )个.| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
 如图,∠A=70°,O是AB上一点,直线OD与AB的夹角∠BOD为80°,要使OD∥AC,直线OD绕点O按逆时针方向至少旋转10度.
如图,∠A=70°,O是AB上一点,直线OD与AB的夹角∠BOD为80°,要使OD∥AC,直线OD绕点O按逆时针方向至少旋转10度.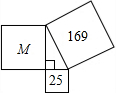 如图,喜羊羊和美羊羊分别做了面积为25和169的两个正方形纸板,村长看到后,把他俩做的正方形和沸羊羊做的正方形M如图放在一起,中间空出的三角形正好是直角三角形,那么正方形M的面积是( )
如图,喜羊羊和美羊羊分别做了面积为25和169的两个正方形纸板,村长看到后,把他俩做的正方形和沸羊羊做的正方形M如图放在一起,中间空出的三角形正好是直角三角形,那么正方形M的面积是( )