题目内容
11. 如图,数轴上点A、B、C所表示的数分别为a、b、c,点C是线段AB的中点,若原点O是线段AC上的任意一点,那么a+b-2c=0.
如图,数轴上点A、B、C所表示的数分别为a、b、c,点C是线段AB的中点,若原点O是线段AC上的任意一点,那么a+b-2c=0.
分析 点A、B、C所表示的数分别为a、b、c,点C是线段AB的中点,由中点公式得:c=$\frac{a+b}{2}$,则a+b=2c,所以a+b-2c=0.
解答 解:∵点A、B、C所表示的数分别为a、b、c,点C是线段AB的中点,
∴由中点公式得:c=$\frac{a+b}{2}$,
∴a+b=2c,
∴a+b-2c=0.
故答案为:0.
点评 题目考查了两点间的距离.根据平面直角坐标系中两点A(x1,y1)、B(x2,y2),则AB两点的中点坐标公式为($\frac{{x}_{1}+{x}_{2}}{2}$,$\frac{{y}_{1}+{y}_{2}}{2}$),数轴上的中点坐标可以看做是X轴上两点坐标即可.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
19.下列方程中,解为x=5的是( )
| A. | 2x+3=5 | B. | $\frac{10}{x}=1$ | C. | 7-(x-1)=3 | D. | 3x-1=2x+6 |
20.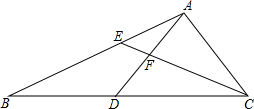 已知:如图,在△ABC中,点D、E分别在边BC、AB上,BD=AD=AC,AD与CE相交于点F,AE2=EF•EC.
已知:如图,在△ABC中,点D、E分别在边BC、AB上,BD=AD=AC,AD与CE相交于点F,AE2=EF•EC.
(1)求证:∠ADC=∠DCE+∠EAF;
(2)求证:AF•AD=AB•EF.
 已知:如图,在△ABC中,点D、E分别在边BC、AB上,BD=AD=AC,AD与CE相交于点F,AE2=EF•EC.
已知:如图,在△ABC中,点D、E分别在边BC、AB上,BD=AD=AC,AD与CE相交于点F,AE2=EF•EC.(1)求证:∠ADC=∠DCE+∠EAF;
(2)求证:AF•AD=AB•EF.
1.两个相似多边形的周长比是2:3,其中较小多边形的面积为4cm2,则较大多边形的面积为( )
| A. | 9cm2 | B. | 16cm2 | C. | 56cm2 | D. | 24cm2 |
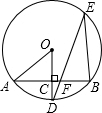 如图,AB是⊙O的一条弦,OD⊥AB,垂足为C,OD交⊙O于点D,点E在☉O上.
如图,AB是⊙O的一条弦,OD⊥AB,垂足为C,OD交⊙O于点D,点E在☉O上.