题目内容
15. 如图,表示抛物线y=ax2+bx+c的一部分图象,它与x轴的一个交点为A,与y轴交于B,则b的取值范围是( )
如图,表示抛物线y=ax2+bx+c的一部分图象,它与x轴的一个交点为A,与y轴交于B,则b的取值范围是( )| A. | -2<b<0 | B. | -1<b<0 | C. | -$\frac{1}{2}$<b<0 | D. | 0<b<0 |
分析 根据函数的图象与两坐标轴的交点可以得到当x=1是a+b+c=2b>-2的取值范围,进一步结合抛物线的开口方向和对称轴确定b的取值范围,两者结合得出答案即可.
解答 解:∵函数y=ax2+bx+c,
∴当x=1时,y=a+b+c,
∵函数图象与两坐标轴交于点(-1,0)和(0,-1),
∴另一个交点位于点(1,0)的右侧,则当x=1是时,函数值一定小于0.
∴当x=1时的函数值一定小于0,
故a+b+c<0,
∵a=b+1>0
∴a+b+c=2b>-2,
∴b>-1,
∵对称轴x=-$\frac{b}{2a}$>0,a>0,
∴b<0,
∴-1<b<0.
故选:B.
点评 本题考查了抛物线与x轴的交点,解题的关键是根据函数图象与两坐标轴的交点求得另一个交点的位置.

练习册系列答案
相关题目
20.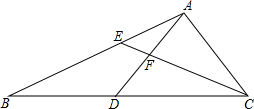 已知:如图,在△ABC中,点D、E分别在边BC、AB上,BD=AD=AC,AD与CE相交于点F,AE2=EF•EC.
已知:如图,在△ABC中,点D、E分别在边BC、AB上,BD=AD=AC,AD与CE相交于点F,AE2=EF•EC.
(1)求证:∠ADC=∠DCE+∠EAF;
(2)求证:AF•AD=AB•EF.
 已知:如图,在△ABC中,点D、E分别在边BC、AB上,BD=AD=AC,AD与CE相交于点F,AE2=EF•EC.
已知:如图,在△ABC中,点D、E分别在边BC、AB上,BD=AD=AC,AD与CE相交于点F,AE2=EF•EC.(1)求证:∠ADC=∠DCE+∠EAF;
(2)求证:AF•AD=AB•EF.
1.两个相似多边形的周长比是2:3,其中较小多边形的面积为4cm2,则较大多边形的面积为( )
| A. | 9cm2 | B. | 16cm2 | C. | 56cm2 | D. | 24cm2 |
7.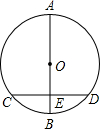 如图,AB为⊙0的直径,弦CD⊥AB于点E,若AE=8,BE=2,则CD=( )
如图,AB为⊙0的直径,弦CD⊥AB于点E,若AE=8,BE=2,则CD=( )
 如图,AB为⊙0的直径,弦CD⊥AB于点E,若AE=8,BE=2,则CD=( )
如图,AB为⊙0的直径,弦CD⊥AB于点E,若AE=8,BE=2,则CD=( )| A. | 6 | B. | 8 | C. | 2$\sqrt{6}$ | D. | 4$\sqrt{5}$ |
4.下列说法中,正确的是( )
| A. | 两条射线组成的图形叫做角 | B. | 两点确定一条直线 | ||
| C. | 两点之间直线最短 | D. | 延长直线AB至C |
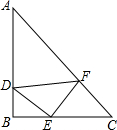 如图,△ABC,△DEF都是等腰直角三角形,D、E、F分别在AB、BC、CA上,已知∠B=∠DEF=90°,AB=BC,DE=EF.
如图,△ABC,△DEF都是等腰直角三角形,D、E、F分别在AB、BC、CA上,已知∠B=∠DEF=90°,AB=BC,DE=EF.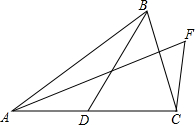 如图,AB=AC,∠ABD=∠CAF,∠F=∠BDC=60°.求证:BD+CF=AF.
如图,AB=AC,∠ABD=∠CAF,∠F=∠BDC=60°.求证:BD+CF=AF.