题目内容
1.如图,点D、E分别在等边△ABC的AB、AC上,且CD>BD,AE>EC,AD和BE相交于点F.(1)若∠BAD=∠CBE,则∠AFE=60°;
(2)若BD=CE,求证:AD=BE;
(3)在(2)的条件下,以AB为边作如图所示的等边△ABG,连接FG,若FG=11,BF=3,请直接写出线段AF的长度为8.
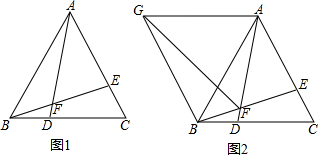
分析 (1)先根据等边三角形各角为60°得:∠ABC=60°,再根据外角定理得:∠AFE=∠ABC=60°;
(2)证明△ABD≌△BCE可得AD=BE;
(3)如图3,作辅助线,构建全等三角形,证明△ABF≌△CBN和△GAF≌△ACN可得AN=FG,可得结论.
解答 解:(1)∵等边△ABC,
∴∠ABC=60°,
∵∠AFE=∠ABE+∠BAD
∴∠AFE=∠BAD+∠ABE=∠ABE+∠CBE=∠ABC=60°,
故答案为:60°;
(2)∵等边△ABC,
∴AB=BC,∠ABD=∠C=60°,
在△ABD和△BCE中,
∵$\left\{\begin{array}{l}{AB=BC}\\{∠ABD=∠C}\\{BD=CE}\end{array}\right.$,
∴△ABD≌△BCE(SAS),
∴AD=BE;
(3)如图3,延长AF至N,使BF=FN=3,连接BN、NC,
∵∠BFN=∠AFE=60°,
∴△BFN是等边三角形,
∴∠FBN=60°,BF=BN=3,
∵∠ABC=60°,
∴∠ABE+∠EBC=∠EBC+∠CBN,
∴∠ABE=∠CBN,
在△ABF和△CBN中,
∵$\left\{\begin{array}{l}{AB=BC}\\{∠ABE=∠CBN}\\{BF=BN}\end{array}\right.$,
∴△ABF≌△CBN,
∴AF=NC,∠BAF=∠BCN,
∴∠BAF+∠GAB=∠BCN+∠ACB,
∵△ABC和△ABG都是等边三角形,
∴∠GAB=∠ACB=60°,AG=AB=AC,
∴∠GAF=∠ACN,
在△GAF和△ACN中,
∵$\left\{\begin{array}{l}{AG=AC}\\{∠GAF=∠ACN}\\{AF=CN}\end{array}\right.$,
∴△GAF≌△ACN(SAS),
∴GF=AN=11,
∴AF+FN=AN=11,
∴AF=11-3=8.
故答案为:8.
点评 本题考查了等边三角形的性质、全等三角形的性质和判定,属于基础题,题意新颖,熟练掌握全等三角形的判定和性质及等边三角形的性质是关键,第三问做出辅助线是关键.

| A. |  | B. |  | C. |  | D. |  |
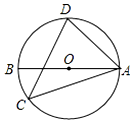 如图,AB为⊙O的直径,CD为⊙O的弦,∠ACD=40°,则∠BAD的度数为50°.
如图,AB为⊙O的直径,CD为⊙O的弦,∠ACD=40°,则∠BAD的度数为50°.