题目内容
16.△ABC中,∠C=90°,AC=8cm,BC=6cm,则△ABC外接圆的半径是5cm.分析 首先运用勾股定理求出斜边AB=10cm,因为直角三角形的外心是斜边的中点,则外接圆的半径是斜边的一半,
解答 解:∵∠C=90°,AC=8cm,BC=6cm,
∴AB=$\sqrt{{8}^{2}+{6}^{2}}$=10cm.
∴△ABC的外接圆半径长R=$\frac{AB}{2}$=$\frac{10}{2}$=5cm.
故答案为:5.
点评 本题考查了三角形的外心的性质.直角三角形的外心是斜边的中点,外接圆的半径是斜边的一半;

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切,切点为D,如果∠A=35°,那么∠C=( )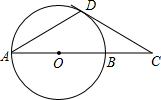

| A. | 55° | B. | 35° | C. | 30° | D. | 20° |
 用边长为a的正方形纸板,制成如图①的一幅七巧板,将它拼成如图②的“小天鹅”图案,其中阴影部分的面积为6cm2,那么a=4cm.
用边长为a的正方形纸板,制成如图①的一幅七巧板,将它拼成如图②的“小天鹅”图案,其中阴影部分的面积为6cm2,那么a=4cm.
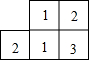 如图是由几个小立方块所搭几何体的从上面看到的形状图,小正方形中的数字表示在该位置小立方块的个数,请画出从正面,左面看到的这个几何体的形状图.
如图是由几个小立方块所搭几何体的从上面看到的形状图,小正方形中的数字表示在该位置小立方块的个数,请画出从正面,左面看到的这个几何体的形状图.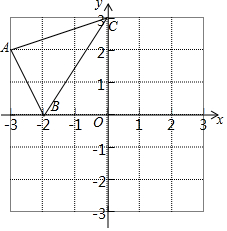 已知在平面直角坐标系中,A(-3,2),B(-2,0),C(0,3)
已知在平面直角坐标系中,A(-3,2),B(-2,0),C(0,3)