题目内容
13.(1)计算:(2$\sqrt{2}$-1)2-(2$\sqrt{2}$+3)(3$\sqrt{2}$-3);(2)解方程:2(x-3)2=(x+3)(x-3).
分析 (1)根据完全平方公式和多项式乘多项式可以解答本题;
(2)根据提公因式法可以解答此方程.
解答 解:(1)(2$\sqrt{2}$-1)2-(2$\sqrt{2}$+3)(3$\sqrt{2}$-3)
=8-4$\sqrt{2}$+1-(12+3$\sqrt{2}$-9)
=8-4$\sqrt{2}$+1-3-3$\sqrt{2}$
=6-7$\sqrt{2}$;
(2)2(x-3)2=(x+3)(x-3)
2(x-3)2-(x+3)(x+3)=0
(x-3)[2(x-3)-(x+3)]=0
(x-3)(x-9)=0
∴x-3=0或x-9=0,
解得,x1=3,x2=9.
点评 本题考查解一元二次方程、二次根式的混合运算,解答本题的关键是明确它们各自的解答方法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.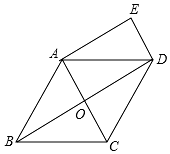 已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
(1)求证:四边形AODE是矩形;
(2)若AB=2$\sqrt{3}$,∠BCD=120°,连接CE,求CE的长.
 已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.(1)求证:四边形AODE是矩形;
(2)若AB=2$\sqrt{3}$,∠BCD=120°,连接CE,求CE的长.
5.如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切,切点为D,如果∠A=35°,那么∠C=( )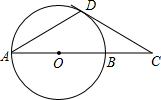

| A. | 55° | B. | 35° | C. | 30° | D. | 20° |
3. 如图,数轴上表示的关于x的一元一次不等式组的解集为( )
如图,数轴上表示的关于x的一元一次不等式组的解集为( )
 如图,数轴上表示的关于x的一元一次不等式组的解集为( )
如图,数轴上表示的关于x的一元一次不等式组的解集为( )| A. | x≥3 | B. | x>3 | C. | 3>x>-1 | D. | -1<x≤3 |
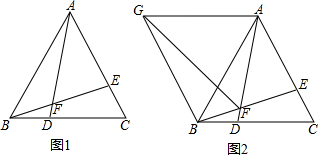
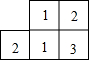 如图是由几个小立方块所搭几何体的从上面看到的形状图,小正方形中的数字表示在该位置小立方块的个数,请画出从正面,左面看到的这个几何体的形状图.
如图是由几个小立方块所搭几何体的从上面看到的形状图,小正方形中的数字表示在该位置小立方块的个数,请画出从正面,左面看到的这个几何体的形状图.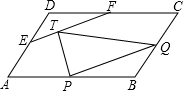 如图,在?ABCD中,分别设P,Q,E,F为边AB,BC,AD,CD的中点,设T为线段EF的三等分点,则△PQT与?ABCD的面积之比是1:4.
如图,在?ABCD中,分别设P,Q,E,F为边AB,BC,AD,CD的中点,设T为线段EF的三等分点,则△PQT与?ABCD的面积之比是1:4.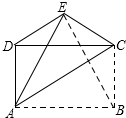 如图,将矩形ABCD沿直线AC折叠,点B落在点E处,连接DE,BE,若△ABE为等边三角形,且S△CDE=$\sqrt{3}$,则CD的长为2$\sqrt{3}$.
如图,将矩形ABCD沿直线AC折叠,点B落在点E处,连接DE,BE,若△ABE为等边三角形,且S△CDE=$\sqrt{3}$,则CD的长为2$\sqrt{3}$.