题目内容
19.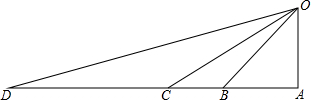 “一号龙卷风”给小岛O造成了较大的破坏,救灾部门迅速组织力量,从仓储D处调集救援物资,计划先用汽车运到与D在同一直线上的C、B、A三个码头中的一处,再用货船运到小岛O.已知:OA⊥AD,∠ODA=15°,∠OCA=30°,∠OBA=45°,CD=20km.若汽车行驶的速度为50km/时,货船航行的速度为25km/时,问这批物资在哪个码头装船,最早运抵小岛O?(在物资搬运能力上每个码头工作效率相同,参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7).
“一号龙卷风”给小岛O造成了较大的破坏,救灾部门迅速组织力量,从仓储D处调集救援物资,计划先用汽车运到与D在同一直线上的C、B、A三个码头中的一处,再用货船运到小岛O.已知:OA⊥AD,∠ODA=15°,∠OCA=30°,∠OBA=45°,CD=20km.若汽车行驶的速度为50km/时,货船航行的速度为25km/时,问这批物资在哪个码头装船,最早运抵小岛O?(在物资搬运能力上每个码头工作效率相同,参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7).
分析 利用三角形外角性质计算出∠COD=15°,则CO=CD=20,在Rt△OCA中利用含30度的直角三角形三边的关系计算出OA=$\frac{1}{2}$OC=10,CA=$\sqrt{3}$OA≈17,在Rt△OBA中利用等腰直角三角形的性质计算出BA=OA=10,OB=$\sqrt{2}$OA≈14,则BC=7,然后根据速度公式分别计算出在三个码头装船,运抵小岛所需的时间,再比较时间的大小进行判断.
解答 解:∵∠OCA=∠D+∠COD,
∴∠COD=30°-15°=15°,
∴CO=CD=20,
在Rt△OCA中,∵∠OCA=30°,
∴OA=$\frac{1}{2}$OC=10,CA=$\sqrt{3}$OA=10$\sqrt{3}$≈17,
在Rt△OBA中,∵∠OBA=45°,
∴BA=OA=10,OB=$\sqrt{2}$OA≈14,
∴BC=17-10=7,
当这批物资在C码头装船,运抵小岛O时,所用时间=$\frac{20}{50}$+$\frac{20}{25}$=1.2(小时);
当这批物资在B码头装船,运抵小岛O时,所用时间=$\frac{20+7}{50}$+$\frac{14}{25}$=1.1(小时);
当这批物资在A码头装船,运抵小岛O时,所用时间=$\frac{20+17}{50}$+$\frac{10}{25}$=1.14(小时);
所以这批物资在B码头装船,最早运抵小岛O.
点评 本题考查了解直角三角形:将实际问题抽象为数学问题(画出平面图形,构造出直角三角形转化为解直角三角形问题).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10. 如图,I是△ABC的内心,AI的延长线和△ABC的外接圆相交于点D,连接BI、BD、DC.下列说法中错误的一项是( )
如图,I是△ABC的内心,AI的延长线和△ABC的外接圆相交于点D,连接BI、BD、DC.下列说法中错误的一项是( )
 如图,I是△ABC的内心,AI的延长线和△ABC的外接圆相交于点D,连接BI、BD、DC.下列说法中错误的一项是( )
如图,I是△ABC的内心,AI的延长线和△ABC的外接圆相交于点D,连接BI、BD、DC.下列说法中错误的一项是( )| A. | 线段DB绕点D顺时针旋转一定能与线段DC重合 | |
| B. | 线段DB绕点D顺时针旋转一定能与线段DI重合 | |
| C. | ∠CAD绕点A顺时针旋转一定能与∠DAB重合 | |
| D. | 线段ID绕点I顺时针旋转一定能与线段IB重合 |
7.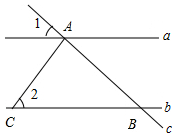 如图,直线a∥b,直线c分别与a、b相交于A、B两点,AC⊥AB于点A,交直线b于点C.已知∠1=42°,则∠2的度数是( )
如图,直线a∥b,直线c分别与a、b相交于A、B两点,AC⊥AB于点A,交直线b于点C.已知∠1=42°,则∠2的度数是( )
 如图,直线a∥b,直线c分别与a、b相交于A、B两点,AC⊥AB于点A,交直线b于点C.已知∠1=42°,则∠2的度数是( )
如图,直线a∥b,直线c分别与a、b相交于A、B两点,AC⊥AB于点A,交直线b于点C.已知∠1=42°,则∠2的度数是( )| A. | 38° | B. | 42° | C. | 48° | D. | 58° |
4.我国古代数学名著《孙子算经》中记载了一道题,大意是:100匹马恰好拉了100片瓦,已知1匹大马能拉3片瓦,3匹小马能拉1片瓦,问有多少匹大马、多少匹小马?若设大马有x匹,小马有y匹,那么可列方程组为( )
| A. | $\left\{\begin{array}{l}{x+y=100}\\{3x+3y=100}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=100}\\{x+3y=100}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=100}\\{3x+\frac{1}{3}y=100}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=100}\\{3x+y=100}\end{array}\right.$ |
18. 如图,O为?ABCD对角线AC,BD的交点,EF经过点O,且与边AD,BC分别交于点E,F,则图中的全等三角形有( )
如图,O为?ABCD对角线AC,BD的交点,EF经过点O,且与边AD,BC分别交于点E,F,则图中的全等三角形有( )
 如图,O为?ABCD对角线AC,BD的交点,EF经过点O,且与边AD,BC分别交于点E,F,则图中的全等三角形有( )
如图,O为?ABCD对角线AC,BD的交点,EF经过点O,且与边AD,BC分别交于点E,F,则图中的全等三角形有( )| A. | 4对 | B. | 5对 | C. | 6对 | D. | 7对 |