题目内容
10. 如图,I是△ABC的内心,AI的延长线和△ABC的外接圆相交于点D,连接BI、BD、DC.下列说法中错误的一项是( )
如图,I是△ABC的内心,AI的延长线和△ABC的外接圆相交于点D,连接BI、BD、DC.下列说法中错误的一项是( )| A. | 线段DB绕点D顺时针旋转一定能与线段DC重合 | |
| B. | 线段DB绕点D顺时针旋转一定能与线段DI重合 | |
| C. | ∠CAD绕点A顺时针旋转一定能与∠DAB重合 | |
| D. | 线段ID绕点I顺时针旋转一定能与线段IB重合 |
分析 根据I是△ABC的内心,得到AI平分∠BAC,BI平分∠ABC,由角平分线的定义得到∠BAD=∠CAD,∠ABI=∠CBI根据三角形外角的性质得到∠BDI=∠DIB,根据等腰三角形的性质得到BD=DI.
解答 解:∵I是△ABC的内心,
∴AI平分∠BAC,BI平分∠ABC,
∴∠BAD=∠CAD,∠ABI=∠CBI,故C正确,不符合题意;
∴$\widehat{BD}$=$\widehat{CD}$,
∴BD=CD,故A正确,不符合题意;
∵∠DAC=∠DBC,
∴∠BAD=∠DBC,
∵∠IBD=∠IBC+∠DBC,∠BID=∠ABI+∠BAD,
∴∠DBI=∠DIB,
∴BD=DI,故B正确,不符合题意;
故选D.
点评 本题考查了三角形的内切圆和内心的,以及等腰三角形的判定与性质,同弧所对的圆周角相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.计算:|-2|+20-(-1)2=( )
| A. | 2 | B. | 0 | C. | 1 | D. | 3 |
18.下面计算正确的是( )
| A. | a4•a2=a8 | B. | b3+b3=b6 | C. | x6÷x2=x3 | D. | (y2)4=y8 |
5. 某校为开展第二课堂,组织调查了本校150名学生各自最喜爱的一项体育活动,制成了如下扇形统计图,则在该被调查的学生中,跑步和打羽毛球的学生人数分别是( )
某校为开展第二课堂,组织调查了本校150名学生各自最喜爱的一项体育活动,制成了如下扇形统计图,则在该被调查的学生中,跑步和打羽毛球的学生人数分别是( )
 某校为开展第二课堂,组织调查了本校150名学生各自最喜爱的一项体育活动,制成了如下扇形统计图,则在该被调查的学生中,跑步和打羽毛球的学生人数分别是( )
某校为开展第二课堂,组织调查了本校150名学生各自最喜爱的一项体育活动,制成了如下扇形统计图,则在该被调查的学生中,跑步和打羽毛球的学生人数分别是( )| A. | 30,40 | B. | 45,60 | C. | 30,60 | D. | 45,40 |
2. 如图,直线l1∥l2,CD⊥AB于点D,∠1=50°,则∠BCD的度数为( )
如图,直线l1∥l2,CD⊥AB于点D,∠1=50°,则∠BCD的度数为( )
 如图,直线l1∥l2,CD⊥AB于点D,∠1=50°,则∠BCD的度数为( )
如图,直线l1∥l2,CD⊥AB于点D,∠1=50°,则∠BCD的度数为( )| A. | 50° | B. | 45° | C. | 40° | D. | 30° |
9.一元二次方程x2-2x+3=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 有一个实数根 | D. | 没有实数根 |


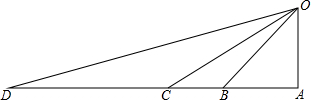 “一号龙卷风”给小岛O造成了较大的破坏,救灾部门迅速组织力量,从仓储D处调集救援物资,计划先用汽车运到与D在同一直线上的C、B、A三个码头中的一处,再用货船运到小岛O.已知:OA⊥AD,∠ODA=15°,∠OCA=30°,∠OBA=45°,CD=20km.若汽车行驶的速度为50km/时,货船航行的速度为25km/时,问这批物资在哪个码头装船,最早运抵小岛O?(在物资搬运能力上每个码头工作效率相同,参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7).
“一号龙卷风”给小岛O造成了较大的破坏,救灾部门迅速组织力量,从仓储D处调集救援物资,计划先用汽车运到与D在同一直线上的C、B、A三个码头中的一处,再用货船运到小岛O.已知:OA⊥AD,∠ODA=15°,∠OCA=30°,∠OBA=45°,CD=20km.若汽车行驶的速度为50km/时,货船航行的速度为25km/时,问这批物资在哪个码头装船,最早运抵小岛O?(在物资搬运能力上每个码头工作效率相同,参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7).