题目内容
12.已知,在平面直角坐标系中,点A(4,0),点B(m,$\frac{\sqrt{3}}{3}$m),点C为线段OA上一点(点O为原点),则AB+BC的最小值为2$\sqrt{3}$.分析 如图,作点A关于直线OB的对称点D,过D作DC⊥OA于C交直线OB于B,则CD=AB+BC的最小值,根据已知条件得到∠AOB=30°,根据直角三角形的性质得到AH=$\frac{1}{2}$OA,于是得到距离.
解答 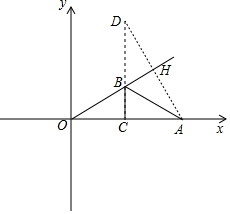 解:∵点B(m,$\frac{\sqrt{3}}{3}$m),
解:∵点B(m,$\frac{\sqrt{3}}{3}$m),
∴点B在y=$\frac{\sqrt{3}}{3}$x的直线上,
如图,作点A关于直线OB的对称点D,过D作DC⊥OA于C交直线OB雨B,
则CD=AB+BC的最小值,
∵B(m,$\frac{\sqrt{3}}{3}$m),
∴tan∠BOC=$\frac{\sqrt{3}}{3}$,
∴∠AOB=30°,
∵∠AHO=90°,
∴AH=$\frac{1}{2}$OA,
∵A(4,0),
∴OA=4,
∴AD=2AH=4,
∴DC=2$\sqrt{3}$,
∴AB+BC的最小值=2$\sqrt{3}$,
故答案为:2$\sqrt{3}$.
点评 本题考查了轴对称-最小距离问题,解直角三角形,正确的作出图形是解题的关键.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
2. 如图,△ABC的三个顶点的坐标分别为A(-3,5),B(-3,0),C(2,0),将△ABC绕点B顺时针旋转一定角度后使A落在y轴上,与此同时顶点C恰好落在y=$\frac{k}{x}$的图象上,则k的值为( )
如图,△ABC的三个顶点的坐标分别为A(-3,5),B(-3,0),C(2,0),将△ABC绕点B顺时针旋转一定角度后使A落在y轴上,与此同时顶点C恰好落在y=$\frac{k}{x}$的图象上,则k的值为( )
 如图,△ABC的三个顶点的坐标分别为A(-3,5),B(-3,0),C(2,0),将△ABC绕点B顺时针旋转一定角度后使A落在y轴上,与此同时顶点C恰好落在y=$\frac{k}{x}$的图象上,则k的值为( )
如图,△ABC的三个顶点的坐标分别为A(-3,5),B(-3,0),C(2,0),将△ABC绕点B顺时针旋转一定角度后使A落在y轴上,与此同时顶点C恰好落在y=$\frac{k}{x}$的图象上,则k的值为( )| A. | -2 | B. | -3 | C. | -4 | D. | -5 |
20.要使式子$\sqrt{x+2}$有意义,则x的取值范围是( )
| A. | x>0 | B. | x≥-2 | C. | x≥2 | D. | x≤2 |
17.因式分解x2y-4y的正确结果是( )
| A. | y(x+4)(x-4) | B. | y(x2-4 ) | C. | y(x-2)2 | D. | y(x+2)(x-2) |
 已知在平面直角坐标系中,△ABC的三个顶点坐标分别为:A(1,4),B(1,1),C(3,2).
已知在平面直角坐标系中,△ABC的三个顶点坐标分别为:A(1,4),B(1,1),C(3,2).