题目内容
2. 如图,△ABC的三个顶点的坐标分别为A(-3,5),B(-3,0),C(2,0),将△ABC绕点B顺时针旋转一定角度后使A落在y轴上,与此同时顶点C恰好落在y=$\frac{k}{x}$的图象上,则k的值为( )
如图,△ABC的三个顶点的坐标分别为A(-3,5),B(-3,0),C(2,0),将△ABC绕点B顺时针旋转一定角度后使A落在y轴上,与此同时顶点C恰好落在y=$\frac{k}{x}$的图象上,则k的值为( )| A. | -2 | B. | -3 | C. | -4 | D. | -5 |
分析 利用点A、B、C的坐标得到AB⊥x轴,AB=5,BC=5,AC=5$\sqrt{2}$,再根据旋转的性质得BA′=AB=5,BC′=BC=5,A′C′=AC=5$\sqrt{2}$,接着确定A′点坐标,设C′(a,b),利用两点间的距离公式得到(a+3)2+b2=25①,a2+(b-4)2=50②,然后解方程组求出a和b得到C′点坐标,最后利用反比例函数图象上点的坐标特征求k的值.
解答  解:∵A(-3,5),B(-3,0),C(2,0),
解:∵A(-3,5),B(-3,0),C(2,0),
∴AB⊥x轴,AB=5,BC=5,
∴AC=5$\sqrt{2}$,
∵将△ABC绕点B顺时针旋转一定角度后使A落在y轴上,
∴BA′=AB=5,BC′=BC=5,A′C′=AC=5$\sqrt{2}$,
在Rt△OBA′中,OA′=$\sqrt{A′{B}^{2}-O{B}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴A′(0,4),
设C′(a,b),
∴BC′2=(a+3)2+b2=25①,A′C′2=a2+(b-4)2=50②,
①-②得b=$\frac{-3a-9}{4}$③,
把③代入①整理得a2+6a-7=0,解得a1=-7(舍去),a2=1,
当a=1时,b=-3,
∴C′(1,-3),
把C′(1,-3)代入y=$\frac{k}{x}$得k=1×(-3)=-3.
故选B.
点评 本题考查了坐标与图形变化-旋转:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.解决本题的关键是利用两点间的距离公式建立方程组.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.某小区开展“节约用水,从我做起”活动,下表是从该小区抽取的10个家庭,8月份比7月份节约用水情况统计:
那么这10个家庭8月份比7月份的节水量的平均数是( )
| 节水量(m3) | 0.2 | 0.3 | 0.4 | 0.5 |
| 家庭数(个) | 1 | 2 | 3 | 4 |
| A. | 0.5m3 | B. | 0.4m3 | C. | 0.35m3 | D. | 0.3m3 |
11. 如图,在五边形ABCDE中,∠A+∠B+∠E=α,DP,CP分别平分∠EDC,∠BCD,则∠P的度数是( )
如图,在五边形ABCDE中,∠A+∠B+∠E=α,DP,CP分别平分∠EDC,∠BCD,则∠P的度数是( )
 如图,在五边形ABCDE中,∠A+∠B+∠E=α,DP,CP分别平分∠EDC,∠BCD,则∠P的度数是( )
如图,在五边形ABCDE中,∠A+∠B+∠E=α,DP,CP分别平分∠EDC,∠BCD,则∠P的度数是( )| A. | 90°+$\frac{1}{2}$α | B. | $\frac{1}{2}α$-90° | C. | $\frac{1}{2}α$ | D. | 540°$-\frac{1}{2}α$ |

 如图,在Rt△ABC中,∠C=90°,∠A=30°,D为AB中点,DE⊥AC于E,AB=8,则DE的长度为( )
如图,在Rt△ABC中,∠C=90°,∠A=30°,D为AB中点,DE⊥AC于E,AB=8,则DE的长度为( )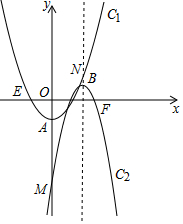 如图,抛物线C1:y1=tx2-1(t>0)和抛物线C2:y2=-4(x-h)2+1(h≥1).
如图,抛物线C1:y1=tx2-1(t>0)和抛物线C2:y2=-4(x-h)2+1(h≥1).