题目内容
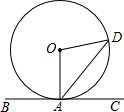 如图,直线BC与⊙O相切于点A,AD是⊙O的弦,连接OD,若∠DAC=50°,则∠ODA的度数为( )
如图,直线BC与⊙O相切于点A,AD是⊙O的弦,连接OD,若∠DAC=50°,则∠ODA的度数为( )| A、30° | B、40° |
| C、50° | D、60° |
考点:切线的性质
专题:
分析:由切线的性质定理可得∠OAC=90°,由此可求出∠OAD的度数,又因为OD=OA,所以∠ODA的度数可求出.
解答:解:∵直线BC与⊙O相切于点A,
∴OA⊥BC,
∴∠OAC=90°,
∵∠DAC=50°,
∴∠OAD=40°,
∵OD=OA,
∴∠ODA=∠OAD=40°,
故选B.
∴OA⊥BC,
∴∠OAC=90°,
∵∠DAC=50°,
∴∠OAD=40°,
∵OD=OA,
∴∠ODA=∠OAD=40°,
故选B.
点评:本题考查了切线的性质定理以及和圆有关的性质,解题的关键是挖掘题目中隐藏条件:圆的半径处处相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
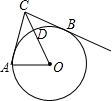 如图,CD,CB分别与⊙O相切于点A,B,连接OA,OC,OC交⊙O于点D,则下列说法中,不一定正确的是( )
如图,CD,CB分别与⊙O相切于点A,B,连接OA,OC,OC交⊙O于点D,则下列说法中,不一定正确的是( )| A、CO平分∠ACB |
| B、OA⊥CA |
| C、CA=CB |
| D、CD=OD |
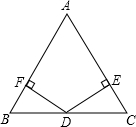 如图,在△ABC中,已知D是BC的中点,DF⊥AB于点F,DE⊥AC于点E,且DF=DE,那么AB=AC吗?你能用学过的知识完成这个问题吗?
如图,在△ABC中,已知D是BC的中点,DF⊥AB于点F,DE⊥AC于点E,且DF=DE,那么AB=AC吗?你能用学过的知识完成这个问题吗?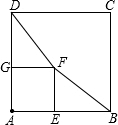 已知正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上.如图,连结DF、BF.
已知正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上.如图,连结DF、BF.