题目内容
 在正方形ABCD中,E是AD的中点,点F在DC上,且DF:FC=1:3,试判断△BEF的形状,并说明理由.
在正方形ABCD中,E是AD的中点,点F在DC上,且DF:FC=1:3,试判断△BEF的形状,并说明理由.考点:勾股定理,勾股定理的逆定理,正方形的性质
专题:
分析:设DF=x,则CF=3x,AB=BC=CD=AD=4x,再根据E是AD的中点得出AE=DE=2x,再根据勾股定理求出BE,EF及BF的长,进而可得出结论.
解答:解:∵DF:FC=1:3,
∴设DF=x,则CF=3x,
∵四边形ABCD是正方形,
∴AB=BC=CD=AD=4x.
∵E是AD的中点,
∴AE=DE=2x,
∴BE2=AE2+AB2,即BE2=(2x)2+(4x)2=20x2;EF2=DE2+DF2,即EF2=(2x)2+x2=5x2;
BF2=BC2+CF2,即BF2=(4x)2+(3x)2=25x2,
∵20x2+5x2=25x2,即BE2+EF2=BF2,
∴△BEF是直角三角形.
∴设DF=x,则CF=3x,
∵四边形ABCD是正方形,
∴AB=BC=CD=AD=4x.
∵E是AD的中点,
∴AE=DE=2x,
∴BE2=AE2+AB2,即BE2=(2x)2+(4x)2=20x2;EF2=DE2+DF2,即EF2=(2x)2+x2=5x2;
BF2=BC2+CF2,即BF2=(4x)2+(3x)2=25x2,
∵20x2+5x2=25x2,即BE2+EF2=BF2,
∴△BEF是直角三角形.
点评:本题考查的是勾股定理,熟知勾股定理及正方形的性质是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
如果直角三角形的三条边长分别是3,4,x,那么x的值为( )
| A、4 | ||
| B、5 | ||
C、4或
| ||
D、5或
|
下列说法中不正确的是( )
| A、由两条射线所组成的图形叫角 |
| B、∠AOB的顶点是点O |
| C、∠AOB和∠BOA表示同一个角 |
| D、角可以看做一条射线绕着端点旋转到加一个位置所形成的图形 |
 如图,已知△ABC和△BDE都为等腰直角三角形,点E在AB上,点F为CD的中点,连接BF.
如图,已知△ABC和△BDE都为等腰直角三角形,点E在AB上,点F为CD的中点,连接BF. 如图,双曲线y=
如图,双曲线y=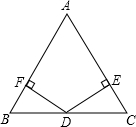 如图,在△ABC中,已知D是BC的中点,DF⊥AB于点F,DE⊥AC于点E,且DF=DE,那么AB=AC吗?你能用学过的知识完成这个问题吗?
如图,在△ABC中,已知D是BC的中点,DF⊥AB于点F,DE⊥AC于点E,且DF=DE,那么AB=AC吗?你能用学过的知识完成这个问题吗?