题目内容
19.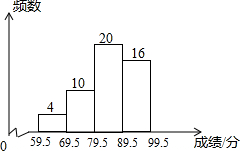 为增强学生环保意识,某中学组织全校2000名学生参加环保知识大赛,比赛成绩均为整数,从中抽取部分同学的成绩进行统计,并绘制成如图统计图.请根据图中提供的信息,解答下列问题:
为增强学生环保意识,某中学组织全校2000名学生参加环保知识大赛,比赛成绩均为整数,从中抽取部分同学的成绩进行统计,并绘制成如图统计图.请根据图中提供的信息,解答下列问题:(1)若抽取的成绩用扇形图来描述,则表示“第三组(79.5~89.5)”的扇形的圆心角为144度;
(2)若成绩在90分以上(含90分)的同学可以获奖,请估计该校约有多少名同学获奖?
(3)某班准备从成绩最好的4名同学(男、女各2名)中随机选取2名同学去社区进行环保宣传,则选出的同学恰好是1男1女的概率为$\frac{2}{3}$.
分析 (1)由第三组(79.5~89.5)的人数即可求出其扇形的圆心角;
(2)首先求出50人中成绩在90分以上(含90分)的同学可以获奖的百分比,进而可估计该校约有多少名同学获奖;
(3)列表得出所有等可能的情况数,找出选出的两名主持人“恰好为一男一女”的情况数,即可求出所求的概率.
解答 解:(1)由直方图可知第三组(79.5~89.5)所占的人数为20人,
所以“第三组(79.5~89.5)”的扇形的圆心角=$\frac{20}{50}×360°$=144°,
故答案为:144;
(2)估计该校获奖的学生数=$\frac{16}{50}×100%$×2000=640(人);
(3)列表如下:
| 男 | 男 | 女 | 女 | |
| 男 | --- | (男,男) | (女,男) | (女,男) |
| 男 | (男,男) | ---- | (女,男) | (女,男) |
| 女 | (男,女) | (男,女) | --- | (女,女) |
| 女 | (男,女) | (男,女) | (女,女) | --- |
则P(选出的两名主持人“恰好为一男一女”)=$\frac{8}{12}$=$\frac{2}{3}$.
故答案为:$\frac{2}{3}$.
点评 本题考查了条形统计图:条形统计图是用线段长度表示数据,根据数量的多少画成长短不同的矩形直条,然后按顺序把这些直条排列起来;从条形图可以很容易看出数据的大小,便于比较.也考查了扇形统计图、列表法与树状图法.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
8.下列运算中,正确的是( )
| A. | a6÷a2=a3 | B. | a-6÷a-2=a-4 | C. | 6a2b÷2ab=3ab | D. | (2xy+y)÷y=2x+y |
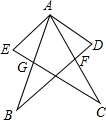 如图,在△ABD和△ACE中,F是AC和DB的交点,G是AB和EC的交点,现有如下4个论断:①AB=AC;②AD=AE;③AF=AG;④AD⊥BD,AE⊥CE.请以其中3个论断为已知条件,1个论断作为结论组成一个正确的说法,并证明其正确性.
如图,在△ABD和△ACE中,F是AC和DB的交点,G是AB和EC的交点,现有如下4个论断:①AB=AC;②AD=AE;③AF=AG;④AD⊥BD,AE⊥CE.请以其中3个论断为已知条件,1个论断作为结论组成一个正确的说法,并证明其正确性.
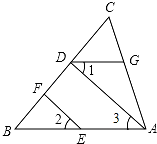 已知:如图,AD⊥BC于点D,∠1=∠2,∠CDG=∠B,求证:EF⊥BC.
已知:如图,AD⊥BC于点D,∠1=∠2,∠CDG=∠B,求证:EF⊥BC.