题目内容
16.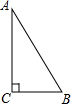 如图,Rt△ABC中,BC=2,AC=2$\sqrt{3}$,则AB长为( )
如图,Rt△ABC中,BC=2,AC=2$\sqrt{3}$,则AB长为( )| A. | 2 | B. | 2$\sqrt{3}$ | C. | 4 | D. | 4$\sqrt{3}$ |
分析 根据勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方列式计算即可.
解答 解:∵在Rt△ABC中,∠ACB=90°,BC=2,AC=2$\sqrt{3}$,
∴AB=$\sqrt{B{C}^{2}+A{C}^{2}}$=$\sqrt{{2}^{2}+(2\sqrt{3})^{2}}$=4.
故选C.
点评 本题考查了勾股定理,掌握如果直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2是解题的关键.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
6.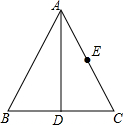 如图,在等边△ABC中,AD平分∠BAC交BC于点D,点E为AC边的中点,BC=2;在AD上有一动点Q,则QC+QE的最小值为( )
如图,在等边△ABC中,AD平分∠BAC交BC于点D,点E为AC边的中点,BC=2;在AD上有一动点Q,则QC+QE的最小值为( )
 如图,在等边△ABC中,AD平分∠BAC交BC于点D,点E为AC边的中点,BC=2;在AD上有一动点Q,则QC+QE的最小值为( )
如图,在等边△ABC中,AD平分∠BAC交BC于点D,点E为AC边的中点,BC=2;在AD上有一动点Q,则QC+QE的最小值为( )| A. | 1 | B. | 1.5 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
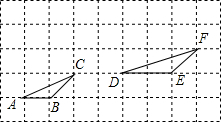 如图,小正方形的边长均为1.图中的两个三角形是否相似?证明你的结论.
如图,小正方形的边长均为1.图中的两个三角形是否相似?证明你的结论. 如图,在Rt△ABC中,∠C=90°,CD⊥AB于D,CD=6,BD=4,则AD=9.
如图,在Rt△ABC中,∠C=90°,CD⊥AB于D,CD=6,BD=4,则AD=9.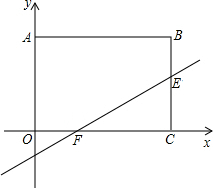 如图所示,在平面直角坐标系中,长方形ABCO的边OA、OC分别在y轴、x轴上,OA=3,OC=4,直线y=$\frac{2}{3}$x-$\frac{2}{3}$与长方形ABCO的边OC、BC分别交于F、E,则△CEF的面积是( )
如图所示,在平面直角坐标系中,长方形ABCO的边OA、OC分别在y轴、x轴上,OA=3,OC=4,直线y=$\frac{2}{3}$x-$\frac{2}{3}$与长方形ABCO的边OC、BC分别交于F、E,则△CEF的面积是( )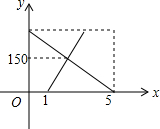 一辆货车从A地出发以一定的速度匀速驶往B地,1小时后,一辆小汽车从B地出发沿同一条路匀速驶往A地,结果小汽车比货车早1小时达到目的地,两车离B地的距离y(km)与所用时间x(h)的函数关系如图所示,则小汽车出发1.5小时后与货车相遇.
一辆货车从A地出发以一定的速度匀速驶往B地,1小时后,一辆小汽车从B地出发沿同一条路匀速驶往A地,结果小汽车比货车早1小时达到目的地,两车离B地的距离y(km)与所用时间x(h)的函数关系如图所示,则小汽车出发1.5小时后与货车相遇.