题目内容
15.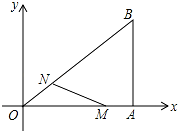 如图,在直角坐标系中,Rt△OAB的直角顶点A在x轴上,OA=4,AB=3.动点M从A出发,以每秒1个单位长度的速度,沿AO向终点O移动;同时点N从点O出发,以每秒1.25个单位长度的速度,沿OB向终点B移动.当两个动点运动了x秒(0<x<4)时,解答下列问题:
如图,在直角坐标系中,Rt△OAB的直角顶点A在x轴上,OA=4,AB=3.动点M从A出发,以每秒1个单位长度的速度,沿AO向终点O移动;同时点N从点O出发,以每秒1.25个单位长度的速度,沿OB向终点B移动.当两个动点运动了x秒(0<x<4)时,解答下列问题:(1)求点N的坐标(用含x的代数式表示);
(2)在两个动点运动过程中,是否存在某一时刻,使△OMN是直角三角形?若存在,求出x的值;若不存在,请说明理由.
(3)当x为何值时,△OMN是等腰三角形.(直接写出x的值)
分析 (1)如图1,作NH⊥OA垂足为H,由NH∥AB得$\frac{ON}{OB}=\frac{OH}{OA}=\frac{NH}{AB}$即可解决问题.
(2)①当∠ONM=90°时,根据△ONM∽△OAB得$\frac{ON}{OA}=\frac{OM}{OB}$即可解决问题;当∠OMN=90°时,由MN∥AB得$\frac{ON}{OB}=\frac{OM}{OA}$即可解决问题.
(3)①当ON=NM时,如图1,由OH=HM=$\frac{1}{2}$OM列出方程x=$\frac{1}{2}$(4-x)求解;②当ON=OM时,得方程1.25x=4-x可以求解;③当OM=MN时,如图2,作MH⊥ON,由△OHM∽△OAB得到$\frac{OH}{OA}=\frac{OM}{OB}$列出方程求解.
解答 解:(1)如图1,作NH⊥OA垂足为H.
在RT△ABC中,∵OA=4,AB=3,
∴AB=$\sqrt{O{A}^{2}+A{B}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5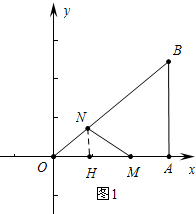
∵∠NHO=∠BAO=90°,
∴NH∥AB,
∴$\frac{ON}{OB}=\frac{OH}{OA}=\frac{NH}{AB}$,
∴$\frac{1.25x}{5}=\frac{OH}{4}=\frac{NH}{3}$,
∴OH=x,HN=$\frac{3}{4}$x,
∴的N坐标(x,$\frac{3}{4}x$).
(2)①当∠ONM=90°时,
∵∠ONM=∠OAB,∠NOM=∠AOB,
∴△ONM∽△OAB,
∴$\frac{ON}{OA}=\frac{OM}{OB}$,
∴$\frac{1.25x}{4}=\frac{4-x}{5}$,
∴x=$\frac{64}{41}$.
②当∠OMN=90°时,∵MN∥AB,
∴$\frac{ON}{OB}=\frac{OM}{OA}$,
∴$\frac{1.25x}{5}=\frac{4-x}{4}$,
∴x=2.
综上所述:x=$\frac{64}{41}$秒或2秒时,△OMN是直角三角形
(3)①当ON=NM时,如图1,∵NH⊥OM,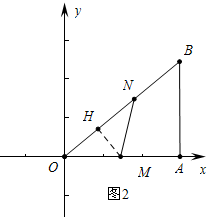
∴OH=HM=$\frac{1}{2}$OM,
∴x=$\frac{1}{2}$(4-x),
∴x=$\frac{4}{3}$.
②当ON=OM时,1.25x=4-x,解得:x=$\frac{16}{9}$.
③当OM=MN时,如图2,作MH⊥ON,则OH=HN,
∵∠MOH=∠BOA,∠MHO=∠OAB,
∴△OHM∽△OAB,
∴$\frac{OH}{OA}=\frac{OM}{OB}$,
∴$\frac{\frac{5}{8}x}{4}=\frac{4-x}{5}$,
x=$\frac{128}{57}$.
综上所述:x=$\frac{4}{3}$秒或$\frac{16}{9}$秒或$\frac{128}{57}$秒时,△OMN是等腰三角形.
点评 本题考查相似三角形的判定和性质、平行线分线段成比例定理、勾股定理等知识,学会转化的思想,用方程去思考是解题的关键.

 阅读快车系列答案
阅读快车系列答案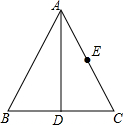 如图,在等边△ABC中,AD平分∠BAC交BC于点D,点E为AC边的中点,BC=2;在AD上有一动点Q,则QC+QE的最小值为( )
如图,在等边△ABC中,AD平分∠BAC交BC于点D,点E为AC边的中点,BC=2;在AD上有一动点Q,则QC+QE的最小值为( )| A. | 1 | B. | 1.5 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |

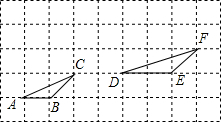 如图,小正方形的边长均为1.图中的两个三角形是否相似?证明你的结论.
如图,小正方形的边长均为1.图中的两个三角形是否相似?证明你的结论.