题目内容
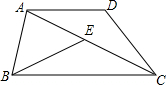 在梯形ABCD中,AD∥BC,连结AC,且AC=BC,在对角线AC上取点E,使CE=AD,连接BE.
在梯形ABCD中,AD∥BC,连结AC,且AC=BC,在对角线AC上取点E,使CE=AD,连接BE.(1)求证:△DAC≌△ECB;
(2)若CA平分∠BCD,且AD=3,求BE的长.
考点:全等三角形的判定与性质
专题:
分析:(1)由平行可得到∠DAC=∠ECB,结合条件可证明△DAC≌△ECB;
(2)由条件可证明DA=DC,结合(1)的结论可得到BE=CD,可求得BE的长.
(2)由条件可证明DA=DC,结合(1)的结论可得到BE=CD,可求得BE的长.
解答:(1)证明:∵AD∥BC,
∴∠DAC=∠ECB,
在△DAC和△ECB中,
,
∴△DAC≌△ECB(SAS);
(2)解:∵CA平分∠BCD,
∴∠ECB=∠DCA,且由(1)可知∠DAC=∠ECB,
∴∠DAC=∠DCA,
∴CD=DA=3,
又∵由(1)可得△DAC≌△ECB,
∴BE=CD=3.
∴∠DAC=∠ECB,
在△DAC和△ECB中,
|
∴△DAC≌△ECB(SAS);
(2)解:∵CA平分∠BCD,
∴∠ECB=∠DCA,且由(1)可知∠DAC=∠ECB,
∴∠DAC=∠DCA,
∴CD=DA=3,
又∵由(1)可得△DAC≌△ECB,
∴BE=CD=3.
点评:本题主要考查全等三角形的判定和性质,掌握全等三角形的判定方法(SSS、SAS、ASA、AAS和HL)和性质(对应边、对应角相等)是解题的关键.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
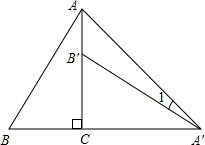 如图,将Rt△ABC绕直角顶点顺时针旋转90°,得到△A′B′C′,连结AA′,若∠1=22°,则∠B的度数是( )
如图,将Rt△ABC绕直角顶点顺时针旋转90°,得到△A′B′C′,连结AA′,若∠1=22°,则∠B的度数是( )| A、68° | B、67° |
| C、62° | D、57° |
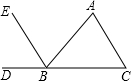 如图,能判定EB∥AC的条件可以是
如图,能判定EB∥AC的条件可以是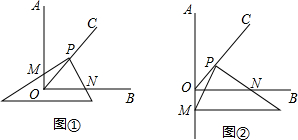
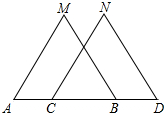 如图,已知A、B、C、D四点在同一直线上,AM=CN,BM=DN,∠M=∠N,
如图,已知A、B、C、D四点在同一直线上,AM=CN,BM=DN,∠M=∠N,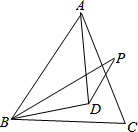 如图,D是等边三角形ABC内一点,DB=DA,BP=AB,∠DPB=∠DBC.求证:∠BPD=30°.
如图,D是等边三角形ABC内一点,DB=DA,BP=AB,∠DPB=∠DBC.求证:∠BPD=30°.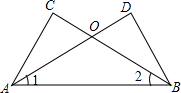 已知:如图,∠1=∠2,∠C=∠D.求证:
已知:如图,∠1=∠2,∠C=∠D.求证: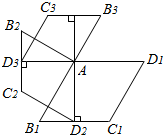 如图,菱形AB1C1D1的边长为1,∠B1=60°,作AD2⊥B1C1于点D2,以AD2为一边,作第二个菱形AB2C2D2,使∠B2=60°;作AD3⊥B2C2于点D2,以AD3为一边作第三个菱形AB3C3D3,使∠B3=60°…依此类推
如图,菱形AB1C1D1的边长为1,∠B1=60°,作AD2⊥B1C1于点D2,以AD2为一边,作第二个菱形AB2C2D2,使∠B2=60°;作AD3⊥B2C2于点D2,以AD3为一边作第三个菱形AB3C3D3,使∠B3=60°…依此类推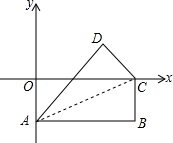 如图,在直角坐标系中,长方形OABC的边OA在y轴的负半轴上,边OC在x轴的正半轴上,点B的坐标为(8,-4),将长方形沿对角线AC翻折,点B落在点D的位置.那么点D的坐标是
如图,在直角坐标系中,长方形OABC的边OA在y轴的负半轴上,边OC在x轴的正半轴上,点B的坐标为(8,-4),将长方形沿对角线AC翻折,点B落在点D的位置.那么点D的坐标是