题目内容
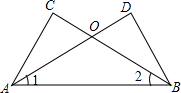 已知:如图,∠1=∠2,∠C=∠D.求证:
已知:如图,∠1=∠2,∠C=∠D.求证:(1)△ABC≌△BAD;
(2)OC=OD.
考点:全等三角形的判定与性质
专题:证明题
分析:(1)利用AAS判定△ABC≌△BAD;
(2)再根据全等三角形的对应边相等求得AD=BC,再由∠1=∠2,可得AO=BO,从而求得OC=OD.
(2)再根据全等三角形的对应边相等求得AD=BC,再由∠1=∠2,可得AO=BO,从而求得OC=OD.
解答:解:(1)在△ABC与△BAD中
∴△ABC≌△BAD(AAS).
(2)∵△ABC≌△BAD,
∴AD=BC,
∵∠1=∠2,
∴AO=BO,
∴AD-AO=BC-BO,
即OC=OD.
|
∴△ABC≌△BAD(AAS).
(2)∵△ABC≌△BAD,
∴AD=BC,
∵∠1=∠2,
∴AO=BO,
∴AD-AO=BC-BO,
即OC=OD.
点评:本题主要考查三角形全等的判定方法及等腰三角形的判定,判定两个三角形全等的一般方法有:SSS、SAS、SSA、HL.本题比较简单,做题时要找准对应关系.

练习册系列答案
相关题目
雅安市雨城区冬季某天早上气温是3℃,到午夜下降了4℃,那么午夜的气温是( )
| A、7℃ | B、1℃ |
| C、-4℃ | D、-1℃ |
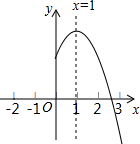 二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,有如下结论:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,有如下结论:①abc<0;②a-b+c>0;③b2>4ac;④3a-2b+c<0,则正确的结论是( )
| A、①②③ | B、①③④ |
| C、②③④ | D、①②③④ |
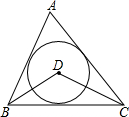 如图,圆O是△ABC的内切圆,∠A=40°,则∠BOC的度数是( )
如图,圆O是△ABC的内切圆,∠A=40°,则∠BOC的度数是( )| A、110° | B、120° |
| C、130° | D、140° |
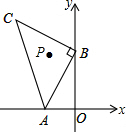 如图,已知点A(a,0),B(0,b),且(a+2)2+|b-4|=0,以B点为直角顶点在第二象限作等腰直角△ABC.
如图,已知点A(a,0),B(0,b),且(a+2)2+|b-4|=0,以B点为直角顶点在第二象限作等腰直角△ABC.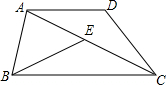 在梯形ABCD中,AD∥BC,连结AC,且AC=BC,在对角线AC上取点E,使CE=AD,连接BE.
在梯形ABCD中,AD∥BC,连结AC,且AC=BC,在对角线AC上取点E,使CE=AD,连接BE.
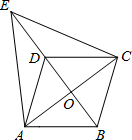 如图,在?ABCD中,对角线AC、BD相交于点O,点E在BD的延长线上,且△EAC是等边三角形.
如图,在?ABCD中,对角线AC、BD相交于点O,点E在BD的延长线上,且△EAC是等边三角形.