题目内容
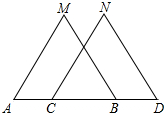 如图,已知A、B、C、D四点在同一直线上,AM=CN,BM=DN,∠M=∠N,
如图,已知A、B、C、D四点在同一直线上,AM=CN,BM=DN,∠M=∠N,证明:(1)AC=BD;(2)MA∥NC.
考点:全等三角形的判定与性质
专题:证明题
分析:根据全等三角形的判定定理SAS推知△ABM≌△CDN.
(1)根据全等三角形的对应边相等知AB=CD,所以有AB-BC=CD-BC,即AC=BD;
(2)由全等三角形的对应角相等知,同位角∠A=∠NCD,所以两直线AM∥CN.
(1)根据全等三角形的对应边相等知AB=CD,所以有AB-BC=CD-BC,即AC=BD;
(2)由全等三角形的对应角相等知,同位角∠A=∠NCD,所以两直线AM∥CN.
解答:证明:(1)在△ABM和△CDN中,
,
∴△ABM≌△CDN(SAS),
∴AB=CD,
∴∴AB-BC=CD-BC,即AC=BD;
(2)由(1)知,△ABM≌△CDN,
∴∠A=∠NCD(全等三角形的对应角相等),
∴AM∥CN(同位角相等,两直线平行).
|
∴△ABM≌△CDN(SAS),
∴AB=CD,
∴∴AB-BC=CD-BC,即AC=BD;
(2)由(1)知,△ABM≌△CDN,
∴∠A=∠NCD(全等三角形的对应角相等),
∴AM∥CN(同位角相等,两直线平行).
点评:本题主要考查了三角形全等的判定与性质、平行线的判定.普通两个三角形全等共有四个定理,即AAS、ASA、SAS、SSS,本题利用了全等三角形的判定定理“SAS“.

练习册系列答案
相关题目
已知|a|=5,|b|=3,则(a+b)(a-b)=( )
| A、4 | B、16 | C、±16 | D、±8 |
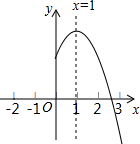 二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,有如下结论:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,有如下结论:①abc<0;②a-b+c>0;③b2>4ac;④3a-2b+c<0,则正确的结论是( )
| A、①②③ | B、①③④ |
| C、②③④ | D、①②③④ |
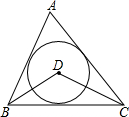 如图,圆O是△ABC的内切圆,∠A=40°,则∠BOC的度数是( )
如图,圆O是△ABC的内切圆,∠A=40°,则∠BOC的度数是( )| A、110° | B、120° |
| C、130° | D、140° |
 如图所示,已知∠A+∠B=180°,则可推的AD∥BC,推理依据是用到了定理
如图所示,已知∠A+∠B=180°,则可推的AD∥BC,推理依据是用到了定理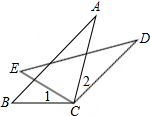 如图,CD=CA,∠1=∠2,EC=BC,与DE相等的线段是哪一条?说明理由.
如图,CD=CA,∠1=∠2,EC=BC,与DE相等的线段是哪一条?说明理由.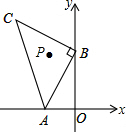 如图,已知点A(a,0),B(0,b),且(a+2)2+|b-4|=0,以B点为直角顶点在第二象限作等腰直角△ABC.
如图,已知点A(a,0),B(0,b),且(a+2)2+|b-4|=0,以B点为直角顶点在第二象限作等腰直角△ABC.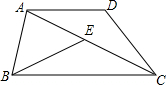 在梯形ABCD中,AD∥BC,连结AC,且AC=BC,在对角线AC上取点E,使CE=AD,连接BE.
在梯形ABCD中,AD∥BC,连结AC,且AC=BC,在对角线AC上取点E,使CE=AD,连接BE.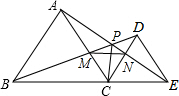 如图,已知点B、C、E在同一条直线上且△ABC与△DEC都是等边三角形,下列结论中,正确的是
如图,已知点B、C、E在同一条直线上且△ABC与△DEC都是等边三角形,下列结论中,正确的是