题目内容
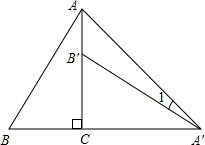 如图,将Rt△ABC绕直角顶点顺时针旋转90°,得到△A′B′C′,连结AA′,若∠1=22°,则∠B的度数是( )
如图,将Rt△ABC绕直角顶点顺时针旋转90°,得到△A′B′C′,连结AA′,若∠1=22°,则∠B的度数是( )| A、68° | B、67° |
| C、62° | D、57° |
考点:旋转的性质
专题:
分析:如图,证明AC=A′C;∠CB′A′=∠B;求出∠CAA′=45°,进而求出∠CB′A′=67°,即可解决问题.
解答: 解:如图,由题意得:△ABC≌△A′B′C,
解:如图,由题意得:△ABC≌△A′B′C,
∴AC=A′C;∠CB′A′=∠B;
∵∠ACA′=90°,
∴∠CAA′=∠CA′A=45°,
∴∠CB′A′=∠CAA′+∠1=45°+22°=67°,
∴∠B=67°.
故选B.
 解:如图,由题意得:△ABC≌△A′B′C,
解:如图,由题意得:△ABC≌△A′B′C,∴AC=A′C;∠CB′A′=∠B;
∵∠ACA′=90°,
∴∠CAA′=∠CA′A=45°,
∴∠CB′A′=∠CAA′+∠1=45°+22°=67°,
∴∠B=67°.
故选B.
点评:该题主要考查了旋转变换的性质、全等三角形的性质等几何知识点及其应用问题;解题的关键是抓住旋转过程中的不变量,动中求静,以静制动.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知|a|=5,|b|=3,则(a+b)(a-b)=( )
| A、4 | B、16 | C、±16 | D、±8 |
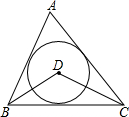 如图,圆O是△ABC的内切圆,∠A=40°,则∠BOC的度数是( )
如图,圆O是△ABC的内切圆,∠A=40°,则∠BOC的度数是( )| A、110° | B、120° |
| C、130° | D、140° |
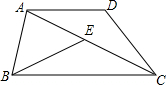 在梯形ABCD中,AD∥BC,连结AC,且AC=BC,在对角线AC上取点E,使CE=AD,连接BE.
在梯形ABCD中,AD∥BC,连结AC,且AC=BC,在对角线AC上取点E,使CE=AD,连接BE. 如图,AB是⊙O的直径,经过圆上点D的直线CD恰使∠ADC=∠B.过点A作直线AB的垂线交BD的延长线于点E,且AB=
如图,AB是⊙O的直径,经过圆上点D的直线CD恰使∠ADC=∠B.过点A作直线AB的垂线交BD的延长线于点E,且AB=
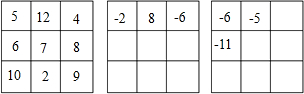
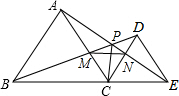 如图,已知点B、C、E在同一条直线上且△ABC与△DEC都是等边三角形,下列结论中,正确的是
如图,已知点B、C、E在同一条直线上且△ABC与△DEC都是等边三角形,下列结论中,正确的是 如图,有一长方形纸片ABCD,AB=5,AD=13,将此长方形纸片折叠,使顶点A落在BC边的A′处,折痕所在直线同时经过边AB,AD(包括端点),设BA′=x,则x的取值范围是
如图,有一长方形纸片ABCD,AB=5,AD=13,将此长方形纸片折叠,使顶点A落在BC边的A′处,折痕所在直线同时经过边AB,AD(包括端点),设BA′=x,则x的取值范围是