题目内容
已知∠AOB=90°,OC是∠AOB的平分线,按以下要求解答问题.
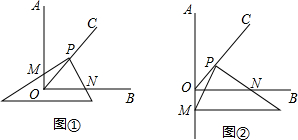
(1)将三角板的直角顶点P在射线OC上移动,两直角边分别与OA,OB交于M,N,如图①,求证:PM=PN;
(2)将三角板的直角顶点P在射线OC上移动,一条直角边与OB交于N,另一条直角边与射线OA的反向延长线交于点M,并猜想此时①中的结论PM=PN是否成立,并说明理由.
(1)将三角板的直角顶点P在射线OC上移动,两直角边分别与OA,OB交于M,N,如图①,求证:PM=PN;
(2)将三角板的直角顶点P在射线OC上移动,一条直角边与OB交于N,另一条直角边与射线OA的反向延长线交于点M,并猜想此时①中的结论PM=PN是否成立,并说明理由.

考点:全等三角形的判定与性质
专题:
分析:(1)过P作PE⊥OA,PF⊥OB,由OC为∠AOB的平分线,利用角平分线定理得到PE=PF,利用同角的余角相等得到一对角相等,利用ASA得到△PME与△PNF全等,利用全等三角形的对应边相等即可得证;
(2)过P作PE⊥OA,PF⊥OB,由OC为∠AOB的平分线,利用角平分线定理得到PE=PF,利用同角的余角相等得到一对角相等,利用ASA得到△PME与△PNF全等,利用全等三角形的对应边相等即可得证.
(2)过P作PE⊥OA,PF⊥OB,由OC为∠AOB的平分线,利用角平分线定理得到PE=PF,利用同角的余角相等得到一对角相等,利用ASA得到△PME与△PNF全等,利用全等三角形的对应边相等即可得证.
解答: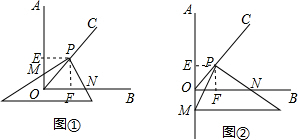 解:(1)过P作PE⊥OA于E,PF⊥OB于F,
解:(1)过P作PE⊥OA于E,PF⊥OB于F,
∵OC是∠AOB的平分线,
∴PE=PF,∠PEM=∠PFN=90°,
∵∠MPE+∠MPF=90°,∠NPF+∠MPF=90°,
∴∠MPE=∠NPF,
在△PME和△PNF中,
,
∴△PME≌△PNF(ASA),
∴PM=PN.
(2)过P作PE⊥OA于E,PF⊥OB于F,
∵OC是∠AOB的平分线,
∴PE=PF,∠PEM=∠PFN=90°,
∵∠MPE+∠MPF=90°,∠NPF+∠MPF=90°,
∴∠MPE=∠NPF,
在△PME和△PNF中,
,
∴△PME≌△PNF(ASA),
∴PM=PN.
 解:(1)过P作PE⊥OA于E,PF⊥OB于F,
解:(1)过P作PE⊥OA于E,PF⊥OB于F,∵OC是∠AOB的平分线,
∴PE=PF,∠PEM=∠PFN=90°,
∵∠MPE+∠MPF=90°,∠NPF+∠MPF=90°,
∴∠MPE=∠NPF,
在△PME和△PNF中,
|
∴△PME≌△PNF(ASA),
∴PM=PN.
(2)过P作PE⊥OA于E,PF⊥OB于F,
∵OC是∠AOB的平分线,
∴PE=PF,∠PEM=∠PFN=90°,
∵∠MPE+∠MPF=90°,∠NPF+∠MPF=90°,
∴∠MPE=∠NPF,
在△PME和△PNF中,
|
∴△PME≌△PNF(ASA),
∴PM=PN.
点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
已知|a|=5,|b|=3,则(a+b)(a-b)=( )
| A、4 | B、16 | C、±16 | D、±8 |
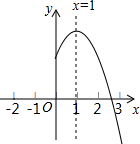 二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,有如下结论:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,有如下结论:①abc<0;②a-b+c>0;③b2>4ac;④3a-2b+c<0,则正确的结论是( )
| A、①②③ | B、①③④ |
| C、②③④ | D、①②③④ |
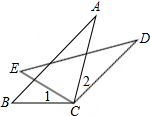 如图,CD=CA,∠1=∠2,EC=BC,与DE相等的线段是哪一条?说明理由.
如图,CD=CA,∠1=∠2,EC=BC,与DE相等的线段是哪一条?说明理由.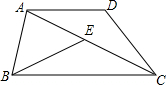 在梯形ABCD中,AD∥BC,连结AC,且AC=BC,在对角线AC上取点E,使CE=AD,连接BE.
在梯形ABCD中,AD∥BC,连结AC,且AC=BC,在对角线AC上取点E,使CE=AD,连接BE.