题目内容
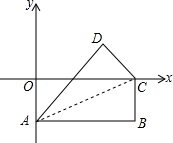 如图,在直角坐标系中,长方形OABC的边OA在y轴的负半轴上,边OC在x轴的正半轴上,点B的坐标为(8,-4),将长方形沿对角线AC翻折,点B落在点D的位置.那么点D的坐标是
如图,在直角坐标系中,长方形OABC的边OA在y轴的负半轴上,边OC在x轴的正半轴上,点B的坐标为(8,-4),将长方形沿对角线AC翻折,点B落在点D的位置.那么点D的坐标是考点:翻折变换(折叠问题),坐标与图形性质
专题:
分析:如图,作辅助线;求出AO=BC=4,OC=AB=8;证明NA=NC(设为λ),ON=8-λ;运用勾股定理求出λ;借助面积公式求出DP=
;运用勾股定理求出DM,即可解决问题.
| 12 |
| 5 |
解答: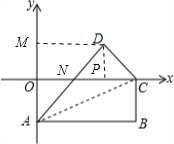 解:如图,过点D作DM⊥y轴于点M;DP⊥x轴于点N;
解:如图,过点D作DM⊥y轴于点M;DP⊥x轴于点N;
由题意得:∠NAC=∠BAC;AD=AB;
∵四边形ABCO为矩形,且点B的坐标为(8,-4),
∴NC∥AB,AO=BC=4,OC=AB=8;
∴∠NCA=∠BAC,∠NAC=∠NCA,
∴NA=NC(设为λ),ON=8-λ;
由勾股定理得:(8-λ)2+42=λ2,
解得:λ=5;
∵S△ADC=
×AD•DC,
S△ADC=
×NC•AO+
NC•DP,
∴
×8×4=
×5×4+
×5×DP,
解得:DP=
;OM=DP=
,
∴AM=
;由勾股定理得:
DM2=AD2-AM2,而AD=8,
∴DM=
,故点D的坐标为(
,
).
故答案为(
,
).
 解:如图,过点D作DM⊥y轴于点M;DP⊥x轴于点N;
解:如图,过点D作DM⊥y轴于点M;DP⊥x轴于点N;由题意得:∠NAC=∠BAC;AD=AB;
∵四边形ABCO为矩形,且点B的坐标为(8,-4),
∴NC∥AB,AO=BC=4,OC=AB=8;
∴∠NCA=∠BAC,∠NAC=∠NCA,
∴NA=NC(设为λ),ON=8-λ;
由勾股定理得:(8-λ)2+42=λ2,
解得:λ=5;
∵S△ADC=
| 1 |
| 2 |
S△ADC=
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得:DP=
| 12 |
| 5 |
| 12 |
| 5 |
∴AM=
| 32 |
| 5 |
DM2=AD2-AM2,而AD=8,
∴DM=
| 24 |
| 5 |
| 24 |
| 5 |
| 12 |
| 5 |
故答案为(
| 24 |
| 5 |
| 12 |
| 5 |
点评:该题主要考查了翻折变换的性质、坐标与图形的关系等几何知识点及其应用问题;解题的关键是数形结合,灵活运用坐标与图形的关系等知识点来分析、判断、解答.

练习册系列答案
相关题目
下列图形不是中心对称图形是( )
A、 |
B、 |
C、 |
D、 |
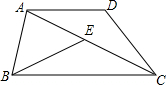 在梯形ABCD中,AD∥BC,连结AC,且AC=BC,在对角线AC上取点E,使CE=AD,连接BE.
在梯形ABCD中,AD∥BC,连结AC,且AC=BC,在对角线AC上取点E,使CE=AD,连接BE.
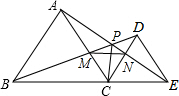 如图,已知点B、C、E在同一条直线上且△ABC与△DEC都是等边三角形,下列结论中,正确的是
如图,已知点B、C、E在同一条直线上且△ABC与△DEC都是等边三角形,下列结论中,正确的是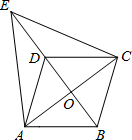 如图,在?ABCD中,对角线AC、BD相交于点O,点E在BD的延长线上,且△EAC是等边三角形.
如图,在?ABCD中,对角线AC、BD相交于点O,点E在BD的延长线上,且△EAC是等边三角形. 如图,用一段长为40米的篱笆围成一个一边靠墙的矩形菜园,墙长为22米.
如图,用一段长为40米的篱笆围成一个一边靠墙的矩形菜园,墙长为22米. 如图,有一长方形纸片ABCD,AB=5,AD=13,将此长方形纸片折叠,使顶点A落在BC边的A′处,折痕所在直线同时经过边AB,AD(包括端点),设BA′=x,则x的取值范围是
如图,有一长方形纸片ABCD,AB=5,AD=13,将此长方形纸片折叠,使顶点A落在BC边的A′处,折痕所在直线同时经过边AB,AD(包括端点),设BA′=x,则x的取值范围是