题目内容
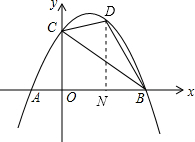
 如图,已知抛物线y=ax2+x+c(a≠0)与x轴交点A(-2,0),点B(6,0),与y轴交于点C.
如图,已知抛物线y=ax2+x+c(a≠0)与x轴交点A(-2,0),点B(6,0),与y轴交于点C.(1)求此抛物线的解析式;
(2)已知点D是第一象限内抛物线上的一动点,求△BCD面积的最大值;
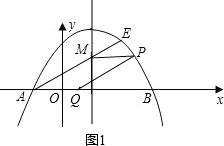
(3)已知点E(4,3),且直线AE交抛物线的对称轴于点M,抛物线上有一动点P,x轴上有一动点Q,是否存在以A,M,P,Q为顶点的四边形为平行四边形?如果存在,请直接写出点Q的坐标;如果不存在,请说明理由.
考点:二次函数综合题
专题:
分析:(1)将点A(-2,0),B(6,0)代入抛物线解析式,可求出a、c的值,继而得出抛物线的解析式;
(2)设出点D的坐标为(m,n),过点D作DN⊥AB于点N,结合题意,用含m或n的式子表示出△BCD的面积,根据二次函数的性质即可得出面积的最大值;
(3)分三种情况进行讨论:
①以AM为边时,如图1、图2,如果MP∥AQ且MP=AQ,那么以A,M,P,Q为顶点的四边形为平行四边形.由P与M的纵坐标相等,将M的纵坐标代入抛物线中求出P的坐标,然后根据M,P的横坐标求出MP的长,即AQ的长,然后根据A的坐标即可求出Q的坐标;
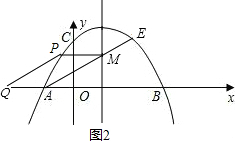
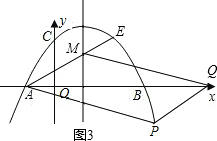
②以AM为边时,如图3、图4,如果AM∥PQ且AM=PQ,那么以A,M,P,Q为顶点的四边形为平行四边形.根据平行四边形的对称性,得出M,P的纵坐标互为相反数,因此可求出P的坐标,然后根据平行四边形的性质及A,M,P的坐标即可求出Q的坐标;
③以AM为对角线时,过M作x轴的平行线交抛物线与P5、P6,由①知,P5(2-2
,2),P6(2+2
,2),根据AM与PQ互相平分,得出AM的中点与PQ的中点重合,由中点坐标公式及A(-2,0),M(2,2),求出AM的中点坐标是(0,1),再利用中点坐标公式即可求出Q的坐标.
(2)设出点D的坐标为(m,n),过点D作DN⊥AB于点N,结合题意,用含m或n的式子表示出△BCD的面积,根据二次函数的性质即可得出面积的最大值;
(3)分三种情况进行讨论:
①以AM为边时,如图1、图2,如果MP∥AQ且MP=AQ,那么以A,M,P,Q为顶点的四边形为平行四边形.由P与M的纵坐标相等,将M的纵坐标代入抛物线中求出P的坐标,然后根据M,P的横坐标求出MP的长,即AQ的长,然后根据A的坐标即可求出Q的坐标;
②以AM为边时,如图3、图4,如果AM∥PQ且AM=PQ,那么以A,M,P,Q为顶点的四边形为平行四边形.根据平行四边形的对称性,得出M,P的纵坐标互为相反数,因此可求出P的坐标,然后根据平行四边形的性质及A,M,P的坐标即可求出Q的坐标;
③以AM为对角线时,过M作x轴的平行线交抛物线与P5、P6,由①知,P5(2-2
| 2 |
| 2 |
解答:解:(1)将A(-2,0),B(6,0)代入抛物线解析式可得:
,
解得:
,
抛物线的解析式为y=-
x2+x+3;
 (2)设点D的坐标为(m,n),则n=-
(2)设点D的坐标为(m,n),则n=-
m2+m+3,
过点D作DN⊥AB于点N,则有:
S△BCD=S梯形ONDC+S△BND-S△BOC
=
(3+n)m+
(6-m)n-
×6×3
=
m+3n-9
=
m+3(-
m2+m+3)-9
=-
m2+
m
=-
(m-3)2+
,
∵-
<0,
∴当m=3时,△BCD的面积最大,最大值是
;
 (3)存在.
(3)存在.
设直线AE的解析式为y=kx+b,
∵A(-2,0),E(4,3),
∴
,解得
,
∴y=
x+1,
∵抛物线y=-
x2+x+3的对称轴是x=
=2,
 ∴当x=2时,y=
∴当x=2时,y=
×2+1=2,
∴M(2,2).
①如图1、图2,当MP∥AQ且MP=AQ时,以A,M,P,Q为顶点的四边形为平行四边形.
∵MP∥AQ,
∴P与M的纵坐标相等,都是2.
将y=2代入y=-
x2+x+3,整理得-
x2+x+1=0,
解得x=2±2
,
∴P点坐标为(2±2
,2),
∵M(2,2),
 ∴MP=2
∴MP=2
,
∴AQ=MP=2
.
当Q在A右侧时,如图1,Q1(2
-2,0),
当Q在A左侧时,如图2,Q2(-2
-2,0);
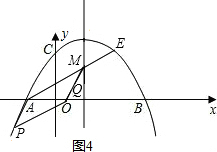
②如图3,当AM∥PQ且AM=PQ时,以A,M,P,Q为顶点的四边形为平行四边形.
∵AQ与PM互相平分,
∴M,P的纵坐标互为相反数,
∵M(2,2),
∴P的纵坐标为-2.
 将y=-2代入y=-
将y=-2代入y=-
x2+x+3,整理得-
x2+x+5=0,
解得x=2±2
∴P点坐标为(2±2
,-2).
当P在y轴右侧时,如图3,P(2+2
,-2).
∵A(-2,0),M(2,2),
∴将A先向右平移4个单位长度,再向上平移2个单位长度可得M,
∵AM∥PQ且AM=PQ,
∴将P先向右平移4个单位长度,再向上平移2个单位长度可得Q.
当P在y轴右侧时,如图3,P(2+2
,-2),Q3(6+2
,0);
当P在y轴左侧时,如图4,P(2-2
,-2),Q4(6-2
,0);
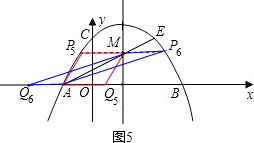 ③如图5,以AM为对角线时,过M作x轴的平行线交抛物线与P5、P6,
③如图5,以AM为对角线时,过M作x轴的平行线交抛物线与P5、P6,
则这两点的纵坐标是2,由①知,P5(2-2
,2),P6(2+2
,2),
∵AM与PQ互相平分,
∴AM的中点与PQ的中点重合.
∵A(-2,0),M(2,2),
∴AM的中点坐标是(0,1).
∴Q5(2
-2,0),Q6(-2-2
,0).
综上所述,存在以A,M,P,Q为顶点的四边形为平行四边形,此时点Q的坐标是:
Q1(2
-2,0),Q2(-2
-2,0),Q3(6+2
,0),Q4(6-2
,0),Q5(2
-2,0),Q6(-2-2
,0).
|
解得:
|
抛物线的解析式为y=-
| 1 |
| 4 |
 (2)设点D的坐标为(m,n),则n=-
(2)设点D的坐标为(m,n),则n=-| 1 |
| 4 |
过点D作DN⊥AB于点N,则有:
S△BCD=S梯形ONDC+S△BND-S△BOC
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 3 |
| 2 |
=
| 3 |
| 2 |
| 1 |
| 4 |
=-
| 3 |
| 4 |
| 9 |
| 2 |
=-
| 3 |
| 4 |
| 27 |
| 4 |
∵-
| 3 |
| 4 |
∴当m=3时,△BCD的面积最大,最大值是
| 27 |
| 4 |
 (3)存在.
(3)存在.设直线AE的解析式为y=kx+b,
∵A(-2,0),E(4,3),
∴
|
|
∴y=
| 1 |
| 2 |
∵抛物线y=-
| 1 |
| 4 |
| -1 | ||
2×(-
|
 ∴当x=2时,y=
∴当x=2时,y=| 1 |
| 2 |
∴M(2,2).
①如图1、图2,当MP∥AQ且MP=AQ时,以A,M,P,Q为顶点的四边形为平行四边形.
∵MP∥AQ,
∴P与M的纵坐标相等,都是2.
将y=2代入y=-
| 1 |
| 4 |
| 1 |
| 4 |
解得x=2±2
| 2 |
∴P点坐标为(2±2
| 2 |
∵M(2,2),
 ∴MP=2
∴MP=2| 2 |
∴AQ=MP=2
| 2 |
当Q在A右侧时,如图1,Q1(2
| 2 |
当Q在A左侧时,如图2,Q2(-2
| 2 |
②如图3,当AM∥PQ且AM=PQ时,以A,M,P,Q为顶点的四边形为平行四边形.
∵AQ与PM互相平分,
∴M,P的纵坐标互为相反数,
∵M(2,2),
∴P的纵坐标为-2.
 将y=-2代入y=-
将y=-2代入y=-| 1 |
| 4 |
| 1 |
| 4 |
解得x=2±2
| 6 |
∴P点坐标为(2±2
| 6 |
当P在y轴右侧时,如图3,P(2+2
| 6 |
∵A(-2,0),M(2,2),
∴将A先向右平移4个单位长度,再向上平移2个单位长度可得M,
∵AM∥PQ且AM=PQ,
∴将P先向右平移4个单位长度,再向上平移2个单位长度可得Q.
当P在y轴右侧时,如图3,P(2+2
| 6 |
| 6 |
当P在y轴左侧时,如图4,P(2-2
| 6 |
| 6 |
 ③如图5,以AM为对角线时,过M作x轴的平行线交抛物线与P5、P6,
③如图5,以AM为对角线时,过M作x轴的平行线交抛物线与P5、P6,则这两点的纵坐标是2,由①知,P5(2-2
| 2 |
| 2 |
∵AM与PQ互相平分,
∴AM的中点与PQ的中点重合.
∵A(-2,0),M(2,2),
∴AM的中点坐标是(0,1).
∴Q5(2
| 2 |
| 2 |
综上所述,存在以A,M,P,Q为顶点的四边形为平行四边形,此时点Q的坐标是:
Q1(2
| 2 |
| 2 |
| 6 |
| 6 |
| 2 |
| 2 |
点评:本题是二次函数的综合题,其中涉及到运用待定系数法求抛物线的解析式,三角形的面积,二次函数的性质,平行四边形的性质,有一定难度.利用分类讨论、数形结合是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列运算中正确的是( )
| A、2x+3y=5xy |
| B、x8÷x2=x4 |
| C、(x2y)3=x6y3 |
| D、2x3•x2=2x6 |
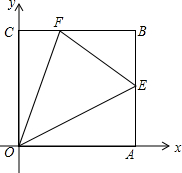 如图,正方形OABC中点B(4,4),点E、F分别在AB、BC上,∠EOF=45°.
如图,正方形OABC中点B(4,4),点E、F分别在AB、BC上,∠EOF=45°.  如图,AD是△ABC的中线,DE⊥AB于点E,DF⊥AC于F,且BE=CF,问AD是否平分∠BAC,如果是,请说明理由.
如图,AD是△ABC的中线,DE⊥AB于点E,DF⊥AC于F,且BE=CF,问AD是否平分∠BAC,如果是,请说明理由. 已知A(-a,0)、B(0,b),且a+b=16,ab=m2-20m+164,C为BO中点,OE⊥AC交AB于E,连AC.
已知A(-a,0)、B(0,b),且a+b=16,ab=m2-20m+164,C为BO中点,OE⊥AC交AB于E,连AC. 如图,抛物线y=ax2+bx+c(a≠0)经过点A(-6,0),B(2,0),C(0,-6)
如图,抛物线y=ax2+bx+c(a≠0)经过点A(-6,0),B(2,0),C(0,-6)
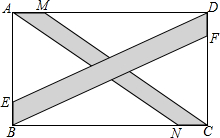 如图,在矩形ABCD中,点E、F在AB、CD上,BF∥DE,若AD=12,AB=7,且AE:EB=5:2,又有点M,N也在AD、BC上,且AM:MD=1:5,AN∥MC,求S空白.
如图,在矩形ABCD中,点E、F在AB、CD上,BF∥DE,若AD=12,AB=7,且AE:EB=5:2,又有点M,N也在AD、BC上,且AM:MD=1:5,AN∥MC,求S空白.