Question

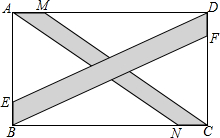如图，在矩形ABCD中，点E、F在AB、CD上，BF∥DE，若AD=12，AB=7，且AE：EB=5：2，又有点M，N也在AD、BC上，且AM：MD=1：5，AN∥MC，求S_空白．
．

Answer 1

考点：矩形的性质

专题：

分析：将空白部分的面积转化为△AED的面积即可求解．

解答：解：∵AE：EB=5：2，且AB=7cm，
∴AE=5cm，EB=2cm，
∵BF∥ED，
∴CF：FD=5：2，即CF=5cm，FD=2cm，
∴△AED和△BCF的面积都等于

1

2

×5×12=30（平方厘米），
∴矩形ABCD的面积为12×7=84（平方厘米），
∴EBFD的面积等于矩形ABCD的面积；
∴△AED的面积=△BCF的面积等于84-30-30=24（平方厘米）．

点评：本题考查了矩形的性质，解题的关键是能够将不规则的几何图形转化为规则的几何图形求解，难度不大．