Question

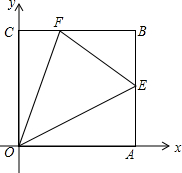如图，正方形OABC中点B（4，4），点E、F分别在AB、BC上，∠EOF=45°．
（1）求证：△BEF的周长为定值；
（2）当AE=1时 求EF的坐标．

Answer 1

考点：全等三角形的判定与性质,坐标与图形性质,勾股定理,正方形的性质

专题：

分析：（1）如图，作辅助线；证明△OAE≌△OCG，得到∠AOE=∠COG，进而得到∠FOG=45°，此为解题的关键性结论；证明△OEF≌△OGF，即可解决问题．
（2）根据（1）中的结论，运用勾股定理求出CF的长度，即可解决问题．

解答：解：（1）如图，延长BF到G，使CG=AE；连接OG；
∵四边形OABC为正方形，且点B坐标为（4，4）
∴OA=OC=4；∠A=∠OCG=90°；
在△OAE与△OCG中，

OA=OC ∠OAE=∠OCG AE=CG

，
∴△OAE≌△OCG（SAS），
∴∠AOE=∠COG（设为α）；OE=OG；
∴∠FOG=∠FOC+∠AOE=90°-45°=45°；
在△OEF与△OGF中，

OE=OG ∠EOF=∠GOF OF=OF

，
∴△OEF≌△OGF（SAS），
∴EF=GF=AE+CF；
∴△BEF的周长=2AB=8，为定值．
（2）设FC=λ，则BF=4-λ，EF=1+λ；BE=4-1=3；
由勾股定理得：（λ+1）²=3²+（4-λ）²，
解得：λ=

12

5

，
故E、F两点的坐标分别为E（4，1）、F（

12

5

，4）．

点评：该题主要考查了正方形的性质、全等三角形的判定及其性质、勾股定理及其应用问题；解题的关键是作辅助线，灵活运用有关定理来分析、判断、解答．