题目内容
2.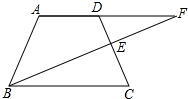 如图,AF∥BC,点D是AF上一点,BF与CD交于点E,点E是CD的中点.
如图,AF∥BC,点D是AF上一点,BF与CD交于点E,点E是CD的中点.(1)求证:△BCE≌△FDE;
(2)连结BD,CF,则BD和FC有何数量和位置关系?试说明理由?
分析 (1)根据平行线的性质得出∠F=∠EBC,根据全等三角形的判定推出即可;
(2)根据全等得出BE=EF,根据全等三角形的判定推出即可.
解答 (1)证明:∵AF∥BC,
∴∠F=∠EBC,
∵点E是CD的中点,
∴DE=CE,
在△BCE和△FDE中,
$\left\{\begin{array}{l}{∠EBC=∠F}\\{∠BEC=∠FED}\\{CE=DE}\end{array}\right.$,
∴△BCE≌△FDE(AAS);
(2)BD=FC,BD∥FC,
理由是:∵△BCE≌△FDE;
∴BE=EF,
在△BDE和△FCE中,
$\left\{\begin{array}{l}{BE=EF}\\{∠BED=∠FEC}\\{DE=EC}\end{array}\right.$,
∴△BDE≌△FCE(SAS),
∴BD=FC,DF=BC,
∴四边形BCFD是平行四边形,
∴BD=FC,BD∥FC.
点评 本题考查了全等三角形的性质和判定,平行线的性质的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,全等三角形的对应边相等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.在$\frac{1}{x}$,$\frac{1}{2}$,$\frac{{x}^{2}+1}{2}$,$\frac{3xy}{π}$,$\frac{3}{x+y}$,a+$\frac{1}{m}$,$\frac{{x}^{2}-9}{x-3}$中分式的个数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
17.下列运算正确的是( )
| A. | a3•a3=2a3 | B. | a4-a2=a2 | C. | (-x)5÷(-x)3=-x2 | D. | (a-b)2(b-a)3=(b-a)5 |
7.若外切两圆的半径分别为1和2,则此两圆的圆心距是( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
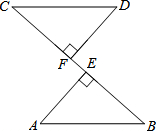 如图,DF=AE,AE⊥BC,DF⊥BC,CE=BF.求证:AB=CD.
如图,DF=AE,AE⊥BC,DF⊥BC,CE=BF.求证:AB=CD. 如图,在矩形ABCD中,已知AB=6cm,BC=8cm.将矩形ABCD绕着点D在桌面上顺时针旋转至A1B1C1D,使其停靠在矩形EFGH的点E处,若∠EDF=30°,则点B的运动路径长为$\frac{10}{3}$πcm.(结果保留π)
如图,在矩形ABCD中,已知AB=6cm,BC=8cm.将矩形ABCD绕着点D在桌面上顺时针旋转至A1B1C1D,使其停靠在矩形EFGH的点E处,若∠EDF=30°,则点B的运动路径长为$\frac{10}{3}$πcm.(结果保留π)