题目内容
7.若外切两圆的半径分别为1和2,则此两圆的圆心距是( )| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
分析 两圆的位置关系有5种:①外离;②外切;③相交;④内切;⑤内含.若d>R+r则两圆相离,若d=R+r则两圆外切,若d=R-r则两圆内切,若R-r<d<R+r则两圆相交,进而求出即可.
解答 解:∵外切两圆的半径分别为1和2,
∴此两圆的圆心距是:1+2=3.
故选:B.
点评 本题主要考查两圆的位置关系.两圆的位置关系有:外离(d>R+r)、内含(d<R-r)、相切(外切:d=R+r或内切:d=R-r)、相交(R-r<d<R+r).

练习册系列答案
相关题目
17.抛物线y=-2(x+6)2+5的顶点坐标是( )
| A. | (6,5) | B. | (-6,5) | C. | (6,-5) | D. | (-2,5) |
18.已知点A(-2,y1)、B(1,y2)、C(4,y3)都在函数y=x2-4x-5的图象上,则比较y1、y2、y3的大小正确的是( )
| A. | y2<y3<y1 | B. | y3<y1<y2 | C. | y1<y3<y2 | D. | y2<y1<y3 |
19. 如图,正方形ABCD中,E是BC边上的一点,以E为圆心,EC为半径的半圆与以A为圆心,AB为半径的圆弧外切,则EB比EA的值为( )
如图,正方形ABCD中,E是BC边上的一点,以E为圆心,EC为半径的半圆与以A为圆心,AB为半径的圆弧外切,则EB比EA的值为( )
 如图,正方形ABCD中,E是BC边上的一点,以E为圆心,EC为半径的半圆与以A为圆心,AB为半径的圆弧外切,则EB比EA的值为( )
如图,正方形ABCD中,E是BC边上的一点,以E为圆心,EC为半径的半圆与以A为圆心,AB为半径的圆弧外切,则EB比EA的值为( )| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{2}{3}$ |
17.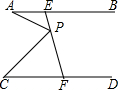 如图,已知AB∥CD,线段EF分别与AB、CD相交于点E、F,P为线段EF上的一点,连接AP、CP,若∠A=25°,∠APC=70°,则∠C的度数为( )
如图,已知AB∥CD,线段EF分别与AB、CD相交于点E、F,P为线段EF上的一点,连接AP、CP,若∠A=25°,∠APC=70°,则∠C的度数为( )
 如图,已知AB∥CD,线段EF分别与AB、CD相交于点E、F,P为线段EF上的一点,连接AP、CP,若∠A=25°,∠APC=70°,则∠C的度数为( )
如图,已知AB∥CD,线段EF分别与AB、CD相交于点E、F,P为线段EF上的一点,连接AP、CP,若∠A=25°,∠APC=70°,则∠C的度数为( )| A. | 45° | B. | 40° | C. | 35° | D. | 30° |
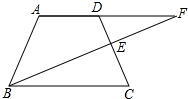 如图,AF∥BC,点D是AF上一点,BF与CD交于点E,点E是CD的中点.
如图,AF∥BC,点D是AF上一点,BF与CD交于点E,点E是CD的中点.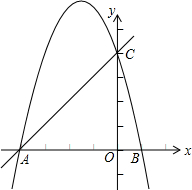 如图,抛物线y=ax2-bx-4a交x轴于点A、B,交y轴于点C,其中点B、C的坐标分别为B(1,0)、C(0,4).
如图,抛物线y=ax2-bx-4a交x轴于点A、B,交y轴于点C,其中点B、C的坐标分别为B(1,0)、C(0,4).